【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )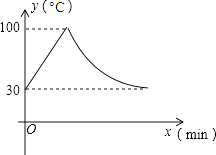
A.7:20
B.7:30
C.7:45
D.7:50
参考答案:
【答案】A
【解析】解:∵开机加热时每分钟上升10℃,
∴从30℃到100℃需要7分钟,
设一次函数关系式为:y=k1x+b,
将(0,30),(7,100)代入y=k1x+b得k1=10,b=30
∴y=10x+30(0≤x≤7),令y=50,解得x=2;
设反比例函数关系式为:y= ![]() ,
,
将(7,100)代入y= ![]() 得k=700,∴y=
得k=700,∴y= ![]() ,
,
将y=30代入y= ![]() ,解得x=
,解得x= ![]() ;
;
∴y= ![]() (7≤x≤
(7≤x≤ ![]() ),令y=50,解得x=14.
),令y=50,解得x=14.
所以,饮水机的一个循环周期为 ![]() 分钟.每一个循环周期内,在0≤x≤2及14≤x≤
分钟.每一个循环周期内,在0≤x≤2及14≤x≤ ![]() 时间段内,水温不超过50℃.
时间段内,水温不超过50℃.
逐一分析如下:
选项A:7:20至8:45之间有85分钟.85﹣ ![]() ×3=15,位于14≤x≤
×3=15,位于14≤x≤ ![]() 时间段内,故可行;
时间段内,故可行;
选项B:7:30至8:45之间有75分钟.75﹣ ![]() ×3=5,不在0≤x≤2及14≤x≤
×3=5,不在0≤x≤2及14≤x≤ ![]() 时间段内,故不可行;
时间段内,故不可行;
选项C:7:45至8:45之间有60分钟.60﹣ ![]() ×2=
×2= ![]() ≈13.3,不在0≤x≤2及14≤x≤
≈13.3,不在0≤x≤2及14≤x≤ ![]() 时间段内,故不可行;
时间段内,故不可行;
选项D:7:50至8:45之间有55分钟.55﹣ ![]() ×2=
×2= ![]() ≈8.3,不在0≤x≤2及14≤x≤
≈8.3,不在0≤x≤2及14≤x≤ ![]() 时间段内,故不可行.
时间段内,故不可行.
综上所述,四个选项中,唯有7:20符合题意.
故选:A.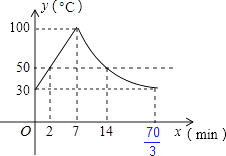
第1步:求出两个函数的解析式;第2步:求出饮水机完成一个循环周期所需要的时间;第3步:求出每一个循环周期内,水温不超过50℃的时间段;第4步:结合4个选择项,逐一进行分析计算,得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏在作⊙O的内接正五边形时,先做了如下几个步骤:
(i)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1;
(ii)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是( )
A.BD2=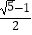 OD
OD
B.BD2=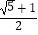 OD
OD
C.BD2=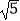 OD
OD
D.BD2=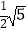 OD
OD -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,以点A为圆心,AB长为半径画弧,交CD于点E,连接AE、BE.作BF⊥AE于点F.
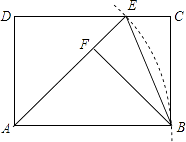
(1)求证:BF=AD;
(2)若EC= ﹣1,∠FEB=67.5°,求扇形ABE的面积(结果保留π).
﹣1,∠FEB=67.5°,求扇形ABE的面积(结果保留π). -
科目: 来源: 题型:
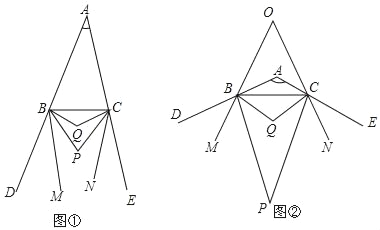
查看答案和解析>>【题目】已知:如图①,BP、CP分别平分△ABC的外角∠CBD、∠BCE,BQ、CQ分别平分∠PBC、∠PCB,BM、CN分别是∠PBD、∠PCE的角平分线.
(1)当∠BAC=40°时,∠BPC= ,∠BQC= ;
(2)当BM∥CN时,求∠BAC的度数;
(3)如图②,当∠BAC=120°时,BM、CN所在直线交于点O,直接写出∠BOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三位同学在操场上互相传球,假设他们相互间传球是等可能的,并且由甲首先开始传球.
(1)经过2次传球后,球仍回到甲手中的概率是;
(2)请用列举法(画树状图或列表)求经过3次传球后,球仍回到甲手中的概率;
(3)猜想并直接写出结论:经过n次传球后,球传到甲、乙这两位同学手中的概率:P(球传到甲手中)和P(球传到乙手中)的大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b与反比例函数y=
 (x<0)的图象交于点A.与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E.己知四边形ADEC的面积为6.
(x<0)的图象交于点A.与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E.己知四边形ADEC的面积为6. 
(1)求k的值;
(2)若AD=3OC,tan∠DAC=2.求点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:

①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
相关试题

