【题目】甲、乙、丙三位同学在操场上互相传球,假设他们相互间传球是等可能的,并且由甲首先开始传球.
(1)经过2次传球后,球仍回到甲手中的概率是;
(2)请用列举法(画树状图或列表)求经过3次传球后,球仍回到甲手中的概率;
(3)猜想并直接写出结论:经过n次传球后,球传到甲、乙这两位同学手中的概率:P(球传到甲手中)和P(球传到乙手中)的大小关系.
参考答案:
【答案】
(1)解:画树状图为: 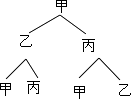
共有4种等可能的结果数,其中球仍回到甲手中的结果数为2,
所以球仍回到甲手中的概率= ![]() =
= ![]() ;
;
故答案为 ![]()
(2)解:画树状图为:
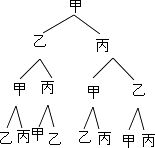
共有8种等可能的结果数,其中球仍回到甲手中的结果数为2,
所以球仍回到甲手中的概率= ![]() =
= ![]()
(3)解:当n为偶数时,P(球传到甲手中)>P(球传到乙手中)的大小关系;
当n为奇数时,P(球传到甲手中)<P(球传到乙手中)的大小关系
【解析】(1)画树状图展示所有4种等可能的结果数,再找出球仍回到甲手中的结果数,然后根据概率公式求解;(2)画树状图展示所有8种等可能的结果数,再找出球仍回到甲手中的结果数,然后根据概率公式求解;(3)利用(1)、(2)的结论讨论:当n为偶数时,P(球传到甲手中)>P(球传到乙手中)的大小关系;当n为奇数时,P(球传到甲手中)<P(球传到乙手中)的大小关系.
【考点精析】根据题目的已知条件,利用列表法与树状图法的相关知识可以得到问题的答案,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,以点A为圆心,AB长为半径画弧,交CD于点E,连接AE、BE.作BF⊥AE于点F.
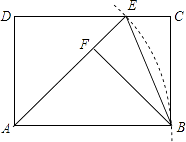
(1)求证:BF=AD;
(2)若EC= ﹣1,∠FEB=67.5°,求扇形ABE的面积(结果保留π).
﹣1,∠FEB=67.5°,求扇形ABE的面积(结果保留π). -
科目: 来源: 题型:
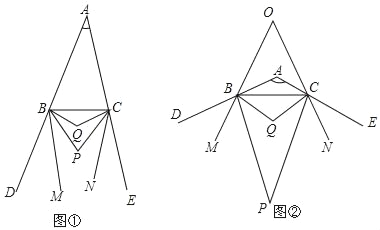
查看答案和解析>>【题目】已知:如图①,BP、CP分别平分△ABC的外角∠CBD、∠BCE,BQ、CQ分别平分∠PBC、∠PCB,BM、CN分别是∠PBD、∠PCE的角平分线.
(1)当∠BAC=40°时,∠BPC= ,∠BQC= ;
(2)当BM∥CN时,求∠BAC的度数;
(3)如图②,当∠BAC=120°时,BM、CN所在直线交于点O,直接写出∠BOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
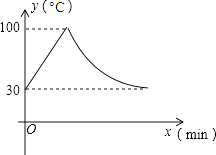
A.7:20
B.7:30
C.7:45
D.7:50 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b与反比例函数y=
 (x<0)的图象交于点A.与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E.己知四边形ADEC的面积为6.
(x<0)的图象交于点A.与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E.己知四边形ADEC的面积为6. 
(1)求k的值;
(2)若AD=3OC,tan∠DAC=2.求点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:

①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD⊥BC,AD=4,CE平分∠ACB交AD于点E.以线段CE为弦作⊙O,且圆心O落在AC上,⊙O交AC于点F,交BC于点G.

(1)求证:AD与⊙O的相切;
(2)若点G为CD的中点,求⊙O的半径;
(3)判断点E能否为AD的中点,若能则求出BC的长,若不能请说明理由.
相关试题

