【题目】(1)如图,平移三角形ABC,使点A平移到点![]() ,画出平移后的三角形
,画出平移后的三角形![]() ;
;
(2)在(1)的条件下,指出点A,B,C 的对应点,并指出AB,BC,AC的对应线段和∠A,∠B, ∠C的对应角.

参考答案:
【答案】(1)见解析;(2)点A,B,C的对应点分别是点A',B',C',线段AB,BC,AC的对应线段分别是A'B',B'C',A'C',∠A,∠B,∠ACB的对应角分别∠A',∠A'B'C',∠A'C'B'
【解析】
根据平移的性质分别得出对应点以及对应线段和对应角即可.
(1)如图所示.
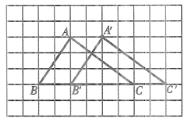
(2)点A,B,C的对应点分别是点A',B',C',线段AB,BC,AC的对应线段分别是A'B',B'C',A'C',∠A,∠B,∠ACB的对应角分别∠A',∠A'B'C',∠A'C'B'.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=
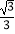 x2﹣
x2﹣ 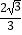 x﹣
x﹣ 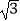 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.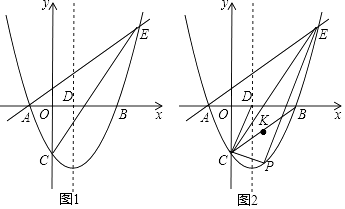
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y=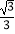 x2﹣
x2﹣ 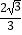 x﹣
x﹣ 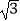 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连结AE,当△ABE时等腰三角形时,求a的值.

-
科目: 来源: 题型:
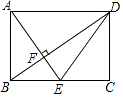
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
A.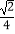
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式
 >
> x﹣1.
x﹣1.(1)当m=1时,求该不等式的解集;
(2)m取何值时,该不等式有解,并求出解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=
 x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为(
x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为( 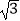 ,3),P是抛物线y=
,3),P是抛物线y=  x2+1上一个动点,则△PMF周长的最小值是( )
x2+1上一个动点,则△PMF周长的最小值是( ) 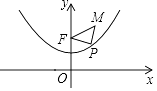
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】认真阅读下面关于三角形内外角平分线的研究片断,完成所提出的问题.
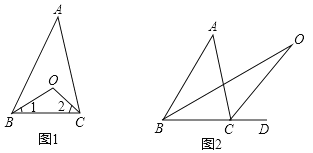
探究1:如图(1)在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+
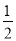 ∠A,理由如下:
∠A,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线,∴∠1=
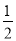 ∠ABC,∠2=
∠ABC,∠2=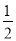 ∠ACB.
∠ACB.∴∠1+∠2=
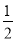 (∠ABC+∠ACB)=
(∠ABC+∠ACB)= 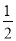 (180°-∠A)=90°-
(180°-∠A)=90°- ∠A.
∠A.∴∠BOC=180°-(∠1+∠2)=180°-(90°-
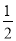 ∠A)=90°+
∠A)=90°+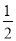 ∠A
∠A探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
相关试题

