【题目】已知抛物线y= ![]() x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为(
x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为( ![]() ,3),P是抛物线y=
,3),P是抛物线y= ![]() x2+1上一个动点,则△PMF周长的最小值是( )
x2+1上一个动点,则△PMF周长的最小值是( ) 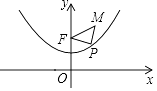
A.3
B.4
C.5
D.6
参考答案:
【答案】C
【解析】解:过点M作ME⊥x轴于点E,交抛物线y= ![]() x2+1于点P,此时△PMF周长最小值, ∵F(0,2)、M(
x2+1于点P,此时△PMF周长最小值, ∵F(0,2)、M( ![]() ,3),
,3),
∴ME=3,FM= ![]() =2,
=2,
∴△PMF周长的最小值=ME+FM=3+2=5.
故选C.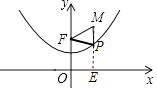
【考点精析】关于本题考查的二次函数的性质和三角形三边关系,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边才能得出正确答案.
-
科目: 来源: 题型:
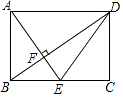
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
A.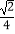
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,平移三角形ABC,使点A平移到点
 ,画出平移后的三角形
,画出平移后的三角形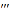 ;
;(2)在(1)的条件下,指出点A,B,C 的对应点,并指出AB,BC,AC的对应线段和∠A,∠B, ∠C的对应角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式
 >
> x﹣1.
x﹣1.(1)当m=1时,求该不等式的解集;
(2)m取何值时,该不等式有解,并求出解集.
-
科目: 来源: 题型:
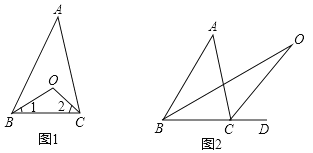
查看答案和解析>>【题目】认真阅读下面关于三角形内外角平分线的研究片断,完成所提出的问题.
探究1:如图(1)在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+
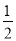 ∠A,理由如下:
∠A,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线,∴∠1=
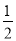 ∠ABC,∠2=
∠ABC,∠2=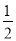 ∠ACB.
∠ACB.∴∠1+∠2=
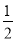 (∠ABC+∠ACB)=
(∠ABC+∠ACB)= 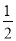 (180°-∠A)=90°-
(180°-∠A)=90°- ∠A.
∠A.∴∠BOC=180°-(∠1+∠2)=180°-(90°-
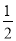 ∠A)=90°+
∠A)=90°+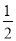 ∠A
∠A探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(直接写出结果):
(1)﹣2+5
(2)﹣17+(﹣3)
(3)(﹣10)﹣(-6)
(4)(﹣1
 )×(﹣12)
)×(﹣12) (5)﹣2×(﹣3)2
(6)﹣1
 ÷(﹣5)
÷(﹣5) (7)﹣1200+(﹣1)200
(8)﹣0.125×(﹣2)3
(9)|﹣
 |
| (10)(-
 )3
)3 -
科目: 来源: 题型:
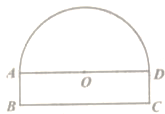
查看答案和解析>>【题目】如图,隧道的截面由半圆和长方形构成,长方形的长BC为8m,宽AB为1m,该隧道内设双向行驶的车道(共有2条车道),若现有一辆货运卡车高4m,宽2.3m。则这辆货运卡车能否通过该隧道?说明理由.
相关试题

