【题目】已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连结AE,当△ABE时等腰三角形时,求a的值.

参考答案:
【答案】(1)8;(2)①DF=17;②a的值为10或12或![]() .
.
【解析】
(1)作AM⊥BC于M,根据三角形的面积公式计算;
(2)①根据勾股定理求出BM、AC,根据平移的性质解答;
②分AB=BE、AB=AE、EA=EB三种情况,根据勾股定理计算即可.
(1)作AM⊥BC于M,

∵△ABC的面积为84,
∴![]() ×BC×AM=84,
×BC×AM=84,
解得,AM=8,即BC边上的高为8;
(2)①在Rt△ABM中,BM=![]() ,
,
∴CM=BC﹣BM=15,
在Rt△ACM中,AC=![]() =17,
=17,
由平移的性质可知,DF=AC=17;
②当AB=BE=10时,a=BE=10;
当AB=AE=10时,BE=2BM=12,
则a=BE=12;
当EA=EB=a时,ME=a﹣6,
在Rt△AME中,AM2+ME2=AE2,
即82+(a﹣6)2=a2,
解得,a=![]() ,
,
则当△ABE时等腰三角形时,a的值为10或12或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线
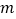 射到平面镜
射到平面镜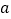 上,被
上,被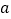 反射到平面镜
反射到平面镜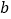 上,又被
上,又被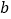 反射,若被
反射,若被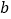 反射出的光线
反射出的光线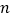 与光线
与光线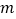 平行,且
平行,且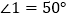 ,则
,则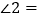 _________,
_________,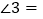 ________.
________.(2)在(1)中,若
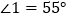 ,则
,则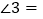 _______;若
_______;若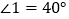 ,则
,则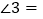 ________;
________;(3)由(1)、(2),请你猜想:当两平面镜
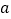 、
、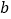 的夹角
的夹角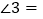 ________时,可以使任何射到平面镜
________时,可以使任何射到平面镜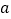 上的光线
上的光线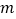 ,经过平面镜
,经过平面镜 、
、 的两次反射后,入射光线
的两次反射后,入射光线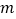 与反射光线
与反射光线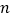 平行.请说明理由.
平行.请说明理由.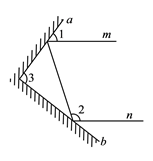
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两名运动员进行射击选拨赛,每人射击10次,其中射击中靶情况如下表:
第一次
第二次
第三次
第四次
第五次
第六次
第七次
第八次
第九次
第十次
甲
7
10
8
10
9
9
10
8
10
9
乙
10
7
10
9
9
10
8
10
7
10
(1)选手甲的成绩的中位数是__________分;选手乙的成绩的众数是__________分;
(2)计算选手甲的平均成绩和方差;
(2)已知选手乙的成绩的方差是1.4,则成绩较稳定的是哪位选手?(直按写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=
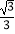 x2﹣
x2﹣ 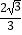 x﹣
x﹣ 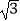 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.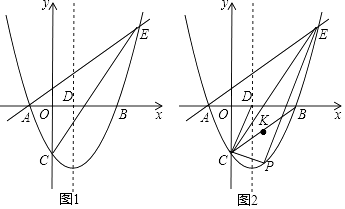
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y=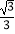 x2﹣
x2﹣ 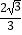 x﹣
x﹣ 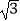 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
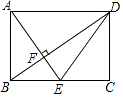
A.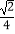
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,平移三角形ABC,使点A平移到点
 ,画出平移后的三角形
,画出平移后的三角形 ;
;(2)在(1)的条件下,指出点A,B,C 的对应点,并指出AB,BC,AC的对应线段和∠A,∠B, ∠C的对应角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式
 >
> x﹣1.
x﹣1.(1)当m=1时,求该不等式的解集;
(2)m取何值时,该不等式有解,并求出解集.
相关试题

