【题目】日前,中国儿童文学作家曹文轩荣获2016年国际儿童读物联盟(IBBY)国际安徒生奖,新安书店抓住契机,以每本20元的价格购进一批畅销书《曹文轩作品集》.销售过程中发现,每月销售量y(本)与销售单价x(元)之间的关系如下表所示,按照表中y与x的关系规律,解决下面的问题:
x | 25 | 28 | 30 | 32 | 35 |
y | 250 | 220 | 200 | 180 | 150 |
(1)试求出y与x的函数关系式.
(2)销售单价在什么范围时,书店能盈利?
(3)如果想要每月获得的利润不低于2000元,那么该书店每月的成本最少需要多少元?(成本=每本进价×销售量)
参考答案:
【答案】
(1)解:设每月销售量y与销售单价x之间的函数关系式为y=kx+b,
由题意,得 ![]() ,
,
解得: ![]() ,
,
∴y与x之间的函数关系式为y=﹣10x+500
(2)解:设书店的利润为w,由题意,得
w=(﹣10x+500)(x﹣20),
w=﹣10x2+700x﹣10000,
当w≥0时,
﹣10x2+700x﹣10000≥0,
(x﹣20)(x﹣50)≤0
解得:20≤x≤50.
答:销售单价在20≤x≤50范围时,书店不亏损
(3)解:由题意,得
﹣10x2+700x﹣10000≥2000,
解得:30≤x≤40
当x=30时,y=200,
∴成本为:200×20=4000,
当x=40时,y=100,
∴成本为:20×100=2000.
∵2000<4000,
∴该书店每月的成本最少需要2000元.
【解析】(1)先分析出函数的类型,x均匀变化,y也均匀变化,那么就是一次函数,可设y=kx+b;(2)构建关于利润的函数,发生盈利也就是利润w≥0,数形结合,可求出范围;(3)由“利润不低于2000”可构建不等式﹣10x2+700x﹣10000≥2000.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,DE⊥AB于E,EF∥BC交AC于F.

(1)求证:△EDF∽△ADE;
(2)猜想:线段DC,DF、DA之间存在什么关系?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
 中,
中, ,垂足为点H,若
,垂足为点H,若 ,
, ,则
,则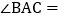 ______
______
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCD中,P为对角线AC上的任意一点,分别连接PB、PD,PE⊥PB,交CD与E.

(1)求证:PE=PD;
(2)当E为CD的中点时,求AP的长;
(3)设AP=x(0<x< ),四边形BPEC的面积为y,求证:y=
),四边形BPEC的面积为y,求证:y=  (
(  ﹣x)2 .
﹣x)2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AC∥DF,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连结CF,再找出CF的中点O,然后连结EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.

以下是他的想法,请你填上根据.小华是这样想的:
因为CF和BE相交于点O,
根据 得出∠COB=∠EOF;
而O是CF的中点,那么CO=FO,又已知 EO=BO,
根据 得出△COB≌△FOE,
根据 得出BC=EF,
根据 得出∠BCO=∠F,
既然∠BCO=∠F,根据 出AB∥DF,
既然AB∥DF,根据 得出∠ACE和∠DEC互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50分才乘上缆车,缆车的平均速度为180米/分,设小亮出发x分后行走的路程为y米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是_________米,他途中休息了___________分;
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度;
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x、y的方程组
 ,给出下列结论:
,给出下列结论:①
 是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④x,y的都为自然数的解有4对.
其中正确的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
相关试题

