【题目】已知:在![]() 中,
中,![]() ,垂足为点H,若
,垂足为点H,若![]() ,
,![]() ,则
,则![]() ______
______![]()
参考答案:
【答案】![]() 或35
或35
【解析】
分析题意,可知本题需分两种情况进行讨论,△ABC为锐角三角形和△ABC为直角三角形;当△ABC为钝角三角形时,过A作BC的垂线,交CB的延长线于点H,由AB+BH=CH,不难得出AB=BC,接下来,再利用三角形外角的性质,可得∠BAC的度数;当△ABC为锐角三角形时,在HC上取D点,使BH=HD,连接AD,再结合AB+BH=CH,不难得出AD=DC,接下来,再利用三角形外角的性质,可得∠DAC的度数;由∠ABH=70°,利用等腰三角形的性质可得出∠BAD的度数,结合上述所得,可得∠BAC的度数.
根据题意画出图形,
当△ABC为钝角三角形时,过A作BC的垂线,交CB的延长线于点H,
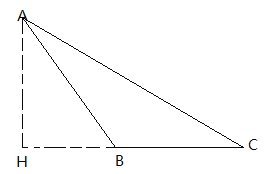
∵AB+BH=CH,HB+BC=CH,
∴AB=BC,
∴∠BAC=∠ACB.
∵∠ABH=70°,
∴∠BAC=∠ACB=35°.
当△ABC为锐角三角形时,在HC上取D点,使BH=HD,连接AD,
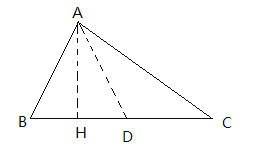
∵AB+BH=HC=HD+DC,BH=HD,
∴AB=DC.
∵AH⊥BD,BH=HD,
∴AB=AD,
∴∠B=∠ADH=70°,
∴∠BAD=40°.
∵AB=DC,AB=AD,
∴AD=CD,
∴∠C=∠DAC,
∴∠ADH=∠C+∠DAC=2∠C,
∴∠DAC=35°,
∴∠BAC=∠BAD+∠DAC=40°+35°=75°.
所以,![]() 35°或75°
35°或75°
故答案为:35°或75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a﹣b+c≥0;
④ 的最小值为3.
的最小值为3.
其中,正确结论的个数为( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求证:角平分线和中线重合的三角形是等腰三角形.
-
科目: 来源: 题型:
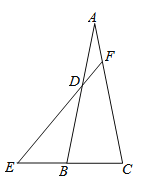
查看答案和解析>>【题目】如图,△ABC是等腰三角形,AB=AC=3,BC=1.点D在AB边上,点E在CB的延长线上,已知AD=1,BE=1,连接ED并延长交AC于点F,则线段AF的长为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了增强学生体质,开设了体育活动小组,并计划购买一些篮球和排球
 已知每个篮球的售价比每个排球的售价多20元,用1100元购进的篮球数量是用450元购进排球数量的2倍.
已知每个篮球的售价比每个排球的售价多20元,用1100元购进的篮球数量是用450元购进排球数量的2倍. 求每个篮球和每个排球的单价各是多少元;
求每个篮球和每个排球的单价各是多少元; 若学校计划购进篮球和排球共50个,且购进的总费用不超过4900元,则学校最多可以购进篮球多少个?
若学校计划购进篮球和排球共50个,且购进的总费用不超过4900元,则学校最多可以购进篮球多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

相关试题

