【题目】按如图的程序进行操作,规定:程序运行从“输入一个值x”到“结果是否>487?”为一次操作. ①如果输入x的值为5,那么操作进行______次才停止.
②如果输入x的值为2k-1,并且操作进行四次才停止,那么k的最大值是________.

参考答案:
【答案】5; 10
【解析】
①将x=5代入3x-2逐次判断是否大于487即可得;
②根据运算程序,列出算式:3x-2,由于运行了四次,所以将每次运算的结果再代入算式,然后再解不等式即可.
解:①当x=5时,3x-2=13<487,
当x=13时,3x-2=37<487,
当x=37时,3x-2=109<487,
当x=109时,3x-2=325<487,
当x=325时,3x-2=973>487,
∴当输入实数x=5时,要操作5次才停止,
故答案为:5;
②第一次的结果为:3x-2,没有输出,则3x-2≤487,
解得:x≤163;
第二次的结果为:3(3x-2)-2=9x-8,没有输出,则9x-8≤487,
解得:x≤55;
第三次的结果为:3(9x-8)-2=27x-26,没有输出,则27x-26≤487,
解得:x≤19;
第四次的结果为:3(27x-26)-2=81x-80,输出,则81x-80>487,
解得:x![]() ;
;
综上可得:7<x≤19.
∵x=2k-1
则7<2k-1≤19,解得:4<k≤10,
则k的最大值是:10
故答案为:10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+
 =0,过C作CB⊥x轴于B.
=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积;
(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
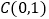 ,直线
,直线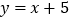 与两坐标轴分别交于A,B两点
与两坐标轴分别交于A,B两点 点D,E分别是OB,AB上的动点,则
点D,E分别是OB,AB上的动点,则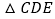 周长的最小值是______.
周长的最小值是______.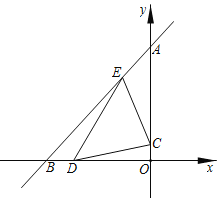
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,河的两岸l1与l2相互平行,A,B是l1上的两点,C,D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.

-
科目: 来源: 题型:
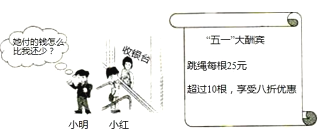
查看答案和解析>>【题目】试根据图中信息,解答下列问题:
(1)购买8根跳绳需________元,购买14根跳绳需________元;
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求小红购买跳绳的根数;若没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:O是坐标原点,P(m,n)(m>0)是函数y=
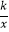 (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+  .
.
(1)当n=1时,求点A的坐标;
(2)若OP=AP,求k的值;
(3)设n是小于20的整数,且k≠ ,求OP2的最小值.
,求OP2的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】现计划把一批货物用一列火车运往某地
 已知这列火车可挂A,B两种不同规格的货车厢共40节,使用A型车厢每节费用6000元,使用B型车厢每节费用为8000元.
已知这列火车可挂A,B两种不同规格的货车厢共40节,使用A型车厢每节费用6000元,使用B型车厢每节费用为8000元. 设运送这批货物的总费用为y元,这列火车挂A型车厢x节,写出y关于x的函数表达式,并求出自变量x的取值范围;
设运送这批货物的总费用为y元,这列火车挂A型车厢x节,写出y关于x的函数表达式,并求出自变量x的取值范围; 已知A型车厢数不少于B型车厢数,运输总费用不低于276000元,问有哪些不同运送方案?
已知A型车厢数不少于B型车厢数,运输总费用不低于276000元,问有哪些不同运送方案?
相关试题

