搜索
【题目】计算：
（1）（﹣8）﹣（﹣15）+（﹣9）﹣（﹣12）
（2）7
+（﹣6.5）+3
+（﹣1.25）+2
（3）（﹣81）÷（﹣2）×
÷（﹣8）
（4）
（5）
（6）
参考答案：
【答案】（1）10；（2）5.5；（3）﹣2；（4）﹣62.5；（5）﹣
；（6）﹣18．
【解析】
（1）（﹣8）﹣（﹣15）+（﹣9）﹣（﹣12）
＝﹣8+15﹣9+12
＝10；
（2）7
+（﹣6.5）+3
+（﹣1.25）+2
＝（7﹣1.25）+（﹣6.5）+（3+2）
＝6﹣6.5+6
＝5.5；
（3）（﹣81）÷（﹣2）×
÷（﹣8）
＝（﹣81）×（﹣）××（﹣
）
＝16×（﹣）
＝﹣2；
（4）
＝
×36﹣×（17.5+2.5）
＝
×36﹣
×36﹣
×36﹣×20
＝6﹣28﹣33﹣7.5
＝﹣62.5；
（5）
＝﹣1﹣0.75×
×（﹣20）×（﹣）
＝﹣1﹣
＝﹣；
（6）
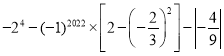
＝﹣16﹣1×（2﹣）﹣
＝﹣16﹣1×
﹣
＝﹣16﹣（
）
＝﹣16﹣2
=﹣18．
-
科目： 来源： 题型：
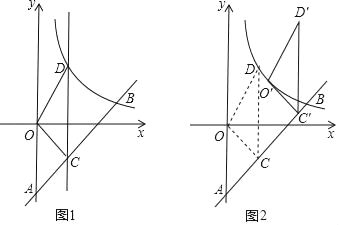
查看答案和解析>>【题目】如图1，一次函数y=kx﹣6（k≠0）的图象与y轴交于点A，与反比例函数y=
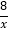（x＞0）的图象交于点B（4，b）．（1）b= ；k= ；
（2）点C是线段AB上一点，过点C且平行于y轴的直线l交该反比例函数的图象于点D，连接OC，OD，BD，若四边形OCBD的面积S四边形OCBD=
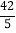，求点C的坐标；（3）将第（2）小题中的△OCD沿射线AB方向平移一定的距离后，得到△O'C'D'，若点O的对应点O'恰好落在该反比例函数图象上（如图2），求此时点D的对应点D'的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，有一个数字迷宫，﹣2在迷宫的第一个拐角，3在第2个拐角，5在第3个拐角，7在第4个拐角，…那么第101个拐角是_____．
-
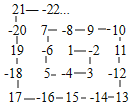
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2﹣5ax﹣4交x轴于A，B两点（点A位于点B的左侧），交y轴于点C，过点C作CD∥AB，交抛物线于点D，连接AC、AD，AD交y轴于点E，且AC=CD，过点A作射线AF交y轴于点F，AB平分∠EAF．
（1）此抛物线的对称轴是 ；
（2）求该抛物线的解析式；
（3）若点P是抛物线位于第四象限图象上一动点，求△APF面积S△APF的最大值，以及此时点P的坐标；
（4）点M是线段AB上一点（不与点A，B重合），点N是线段AD上一点（不与点A，D重合），则两线段长度之和：MN+MD的最小值是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：若在一个两位正整数N的个位数字与十位数字之间添上数字6，组成一个新的三位数，我们称这个三位数为N的“至善数”，如34的“至善数为364”；若将一个两位正整数M加6后得到一个新数，我们称这个新数为M的“明德数”，如34的“明德数为40”．
（1）30的“至善数”是 ，“明德数”是 ．
（2）求证：对任意一个两位正整数A，其“至善数”与“明德数”之差能被9整除；
（3）若一个两位正整数B的明德数的各位数字之和是B的至善数各位数字之和的一半，求B的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】随着通讯技术迅猛发展，人与人之间的沟通方式更多样、便捷．某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷（每人必选且只选一种），在全校范围内随机调查了部分学生，将统计结果绘制了如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：
（1）这次统计共抽查了 名学生；在扇形统计图中，表示“QQ”的扇形圆心角的度数为 ；
（2）将条形统计图补充完整；
（3）该校共有1500名学生，请估计该校最喜欢用“微信”进行沟通的学生有多少名？
（4）某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系，请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明从家出发，沿一条直道跑步，经过一段时间原路返回，刚好在第16分钟回到家中．设小明出发第t分钟的速度为v米/分，离家的距离为s米．v与t之间的部分图象、s与t之间的部分图象分别如图1与图2（图象没画完整，其中图中的空心圈表示不包含这一点），则当小明离家600米时，所用的时间是（ ）分钟．
A. 4.5B. 8.25C. 4.5 或8.25D. 4.5 或 8.5
相关试题
