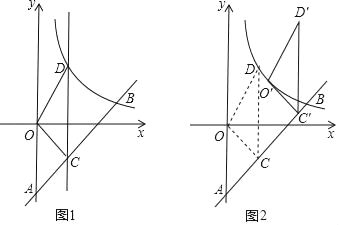
【题目】如图1,一次函数y=kx﹣6(k≠0)的图象与y轴交于点A,与反比例函数y=![]() (x>0)的图象交于点B(4,b).
(x>0)的图象交于点B(4,b).
(1)b= ;k= ;
(2)点C是线段AB上一点,过点C且平行于y轴的直线l交该反比例函数的图象于点D,连接OC,OD,BD,若四边形OCBD的面积S四边形OCBD=![]() ,求点C的坐标;
,求点C的坐标;
(3)将第(2)小题中的△OCD沿射线AB方向平移一定的距离后,得到△O'C'D',若点O的对应点O'恰好落在该反比例函数图象上(如图2),求此时点D的对应点D'的坐标.
参考答案:
【答案】(1)2;2;(2)C(![]() ,﹣1);(3)D′(
,﹣1);(3)D′(![]() ,
,![]() ).
).
【解析】分析:(1)利用待定系数法把点B(4,b)代入y=![]() 即可求解;(2)设C(m,2m-6)(0<m<4),则D(m,
即可求解;(2)设C(m,2m-6)(0<m<4),则D(m,![]() ),根据四边形的面积构建方程即可解决问题;(3)根据一次函数,利用方程组求出点O的坐标,即可解决问题.
),根据四边形的面积构建方程即可解决问题;(3)根据一次函数,利用方程组求出点O的坐标,即可解决问题.
详解:(1)把点B(4,b)代入y=![]() 中,得到b=2,
中,得到b=2,
∴B(4,2)代入y=kx﹣6中,得到k=2,
故答案为2,2;
(2)设C(m,2m﹣6)(0<m<4),则D(m,![]() ),
),
∴CD=![]() ﹣2m+6,
﹣2m+6,
∵S四边形OCBD=![]() ,
,
∴![]() CDxB=
CDxB=![]() ,
,
即![]() (
(![]() ﹣2m+6)×4=
﹣2m+6)×4=![]() ,
,
∴10m2﹣9m﹣40=0,
∴m1=![]() ,m2=﹣
,m2=﹣![]() ,
,
经检验:m1=![]() ,m2=﹣
,m2=﹣![]() 是原方程的解,
是原方程的解,
∵0<m<4,
∴m=![]() ,
,
∴C(![]() ,﹣1).
,﹣1).
(3)由平移可知:OO′∥AB,
∴直线OO′的解析式为y=2x,
由![]() ,解得
,解得![]() 或
或![]() (舍弃),
(舍弃),
∴O′(2,4),
∴D′(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由一些奇数排成的数阵.

(1)设框中的第一个数为
 ,则框中这四个数和为 .
,则框中这四个数和为 .(2)若这样框出的四个数的和
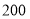 ,求这四个数;
,求这四个数;(3)是否存在这样的四个数,使它们的和为
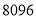 ?请说明理由.
?请说明理由. -
科目: 来源: 题型:
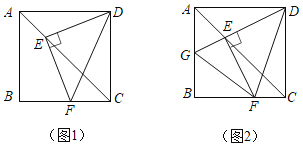
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E,F分别是AC,BC上的点,且满足DE⊥EF,垂足为点E,连接DF.
(1)求∠EDF= (填度数);
(2)延长DE交AB于点G,连接FG,如图2,猜想AG,GF,FC三者的数量关系,并给出证明;
(3)①若AB=6,G是AB的中点,求△BFG的面积;
②设AG=a,CF=b,△BFG的面积记为S,试确定S与a,b的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:若
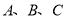 为数轴上三点,若点
为数轴上三点,若点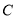 到
到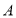 的距离是点
的距离是点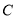 到
到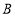 的距离
的距离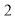 倍,我们就称点
倍,我们就称点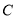 是
是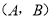 的巧点.若
的巧点.若 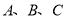 为数轴上三点,若点
为数轴上三点,若点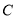 到
到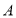 的距离是点
的距离是点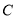 到
到 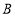 的距离一半,我们就称点
的距离一半,我们就称点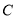 是
是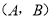 的妙点.如图,点
的妙点.如图,点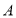 表示的数为
表示的数为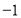 ,点
,点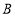 表示的数为
表示的数为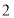 ,表示
,表示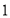 的点
的点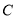 到点
到点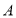 的距离是
的距离是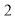 ,到点
,到点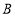 的距离是
的距离是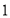 ,那么点
,那么点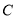 是
是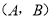 的巧点,点
的巧点,点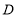 是
是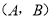 的妙点.
的妙点.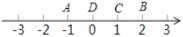
知识运用:
(1)如图 1,点
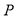 表示的数是
表示的数是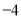 ,点
,点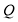 表示的数是
表示的数是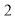 ,点
,点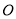 表示的数是
表示的数是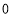 ,那么点
,那么点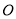 是(
是(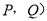 的( )
的( )
A.巧点 B. 妙点 C. 无法确定
(2)如图 2,
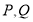 为数轴上两点,点
为数轴上两点,点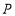 所表示的数为
所表示的数为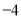 ,点
,点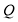 所表示的数为
所表示的数为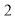 ,则(
,则(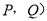 的巧点表示的数是 ;
的巧点表示的数是 ;

拓展提升
(3)如图 3,
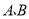 为数轴上两点,点
为数轴上两点,点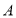 所表示的数为
所表示的数为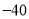 ,点
,点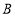 所表示的数为
所表示的数为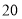 .现有一只电子蚂蚁P从点
.现有一只电子蚂蚁P从点  出发,以每
出发,以每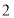 秒单位的速度向右运动,到达点
秒单位的速度向右运动,到达点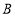 停止. 当经过几秒时,
停止. 当经过几秒时,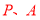 和
和 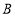 其有一个点为其余两点的巧点? (请直接写出结果)
其有一个点为其余两点的巧点? (请直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,有一个数字迷宫,﹣2在迷宫的第一个拐角,3在第2个拐角,5在第3个拐角,7在第4个拐角,…那么第101个拐角是_____.
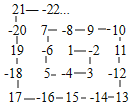
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣5ax﹣4交x轴于A,B两点(点A位于点B的左侧),交y轴于点C,过点C作CD∥AB,交抛物线于点D,连接AC、AD,AD交y轴于点E,且AC=CD,过点A作射线AF交y轴于点F,AB平分∠EAF.
(1)此抛物线的对称轴是 ;
(2)求该抛物线的解析式;
(3)若点P是抛物线位于第四象限图象上一动点,求△APF面积S△APF的最大值,以及此时点P的坐标;
(4)点M是线段AB上一点(不与点A,B重合),点N是线段AD上一点(不与点A,D重合),则两线段长度之和:MN+MD的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣8)﹣(﹣15)+(﹣9)﹣(﹣12)
(2)7
 +(﹣6.5)+3
+(﹣6.5)+3 +(﹣1.25)+2
+(﹣1.25)+2
(3)(﹣81)÷(﹣2
 )×
)× ÷(﹣8)
÷(﹣8)(4)
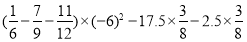
(5)
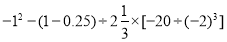
(6)

相关试题

