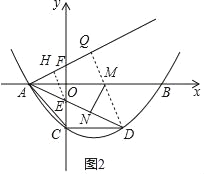
【题目】如图,抛物线y=ax2﹣5ax﹣4交x轴于A,B两点(点A位于点B的左侧),交y轴于点C,过点C作CD∥AB,交抛物线于点D,连接AC、AD,AD交y轴于点E,且AC=CD,过点A作射线AF交y轴于点F,AB平分∠EAF.
(1)此抛物线的对称轴是 ;
(2)求该抛物线的解析式;
(3)若点P是抛物线位于第四象限图象上一动点,求△APF面积S△APF的最大值,以及此时点P的坐标;
(4)点M是线段AB上一点(不与点A,B重合),点N是线段AD上一点(不与点A,D重合),则两线段长度之和:MN+MD的最小值是 .

参考答案:
【答案】(1)直线x=![]() ;(2)抛物线解析式为y=
;(2)抛物线解析式为y=![]() x2﹣
x2﹣![]() x﹣4;(3)当x=4时,S△APF的最大值为
x﹣4;(3)当x=4时,S△APF的最大值为![]() ,此时P点坐标为(4,﹣
,此时P点坐标为(4,﹣![]() );(4)
);(4)![]() .
.
【解析】分析:(1)直接利用抛物线的对称轴方程求解;(2)先确定C(0,4)再利用对称性得到D(5,-4),从而得到CD=AC=5,然后求出A点的坐标,再把A点坐标代入y=ax-5ax-4中求出a即可;(3)作PQ∥y轴交AF于Q,如图1,先利用待定系数法确定直线AD的解析式为y=﹣![]() x﹣
x﹣![]() 得到E(0,-
得到E(0,-![]() ),再根据等腰三角形的三线合一确定F(0,
),再根据等腰三角形的三线合一确定F(0,![]() ),则易得直线AF的解析式为y=
),则易得直线AF的解析式为y=![]() ,设P(x,
,设P(x,![]() -4)(0<x<8=,则Q(x,
-4)(0<x<8=,则Q(x,![]() ) ,所以PQ=
) ,所以PQ= ![]() ,然后利用三角形面积公式,根据
,然后利用三角形面积公式,根据![]() 可表示出
可表示出![]() ,最后利用二次函数的性质解决问题;
,最后利用二次函数的性质解决问题;
(4)作DQ⊥AF于Q,交x轴于M,作MN⊥AD于N,EH⊥AF于H,如图2,利用两点之间线段最短和垂线段最短判断此时MN+MD的值最小,再利用面积法求出EH,然后利用平行线分线段成比例定理计算DQ即可.
详解:(1)抛物线的对称轴为直线x=﹣![]() =
=![]() ;
;
(2)当x=0时,y=ax2﹣5ax﹣4=﹣4,则C(0,﹣4);
∵CD∥x轴,
∴点C与点D关于直线x=![]() 对称,
对称,
∴D(5,﹣4),CD=5,
∵AC=CD,
∴AC=5,
在Rt△AOC中,OA=![]() =3,
=3,
∴A(﹣3,0),
把A(﹣3,0)代入y=ax2﹣5ax﹣4得9a+15a﹣4=0,解得a=![]() ,
,
∴抛物线解析式为y=![]() x2﹣
x2﹣![]() x﹣4;
x﹣4;
(3)作PQ∥y轴交AF于Q,如图1,
当y=0时,![]() x2﹣
x2﹣![]() x﹣4=0,解得x1=﹣3,x2=8,则P(8,0),
x﹣4=0,解得x1=﹣3,x2=8,则P(8,0),
设直线AD的解析式为y=kx+b,
把A(﹣3,0),D(5,﹣4)代入得![]() ,解得
,解得![]() ,
,
∴直线AD的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
当x=0时,y=﹣![]() x﹣
x﹣![]() =﹣
=﹣![]() ,则E(0,﹣
,则E(0,﹣![]() ),
),
∵AB平分∠EAF,AO⊥EF,
∴OF=OE=![]() ,
,
∴F(0,![]() ),
),
易得直线AF的解析式为y=![]() x+
x+![]() ,
,
设P(x,![]() x2﹣
x2﹣![]() x﹣4)(0<x<8),则Q(x,
x﹣4)(0<x<8),则Q(x,![]() x+
x+![]() ),
),
∴PQ=![]() x+
x+![]() ﹣(
﹣(![]() x2﹣
x2﹣![]() x﹣4)=﹣
x﹣4)=﹣![]() x2+
x2+![]() x+
x+![]() ,
,
∴S△APF=S△PAQ﹣S△PFQ=![]() 3PQ=﹣
3PQ=﹣![]() x2+2x+
x2+2x+![]() =﹣
=﹣![]() (x﹣4)2+
(x﹣4)2+![]() ,
,
当x=4时,S△APF的最大值为![]() ,此时P点坐标为(4,﹣
,此时P点坐标为(4,﹣![]() );
);
(4)作DQ⊥AF于Q,交x轴于M,作MN⊥AD于N,EH⊥AF于H,如图2,
∵AB平分∠EAF,
∴MQ=MN,
∴MN+MD=DQ,
∴此时MN+MD的值最小,
∵A(﹣3,0),E(0,﹣![]() ),D(5,﹣4),
),D(5,﹣4),
∴AE=![]() =
=![]() ,AD=
,AD=![]() =4
=4![]() ,
,
∵![]() OAEF=
OAEF=![]() EHAF,
EHAF,
∴EH=![]() =
=![]() ,
,
∵EH∥DQ,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴DQ=![]() ,
,
即MN+MD的最小值是![]() .
.
故答案为直线x=![]() ;
;![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:若
 为数轴上三点,若点
为数轴上三点,若点 到
到 的距离是点
的距离是点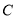 到
到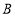 的距离
的距离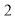 倍,我们就称点
倍,我们就称点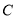 是
是 的巧点.若
的巧点.若  为数轴上三点,若点
为数轴上三点,若点 到
到 的距离是点
的距离是点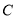 到
到 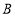 的距离一半,我们就称点
的距离一半,我们就称点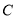 是
是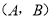 的妙点.如图,点
的妙点.如图,点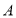 表示的数为
表示的数为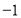 ,点
,点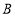 表示的数为
表示的数为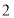 ,表示
,表示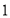 的点
的点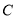 到点
到点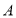 的距离是
的距离是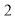 ,到点
,到点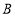 的距离是
的距离是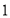 ,那么点
,那么点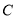 是
是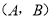 的巧点,点
的巧点,点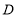 是
是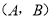 的妙点.
的妙点.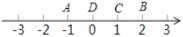
知识运用:
(1)如图 1,点
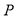 表示的数是
表示的数是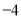 ,点
,点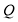 表示的数是
表示的数是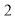 ,点
,点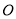 表示的数是
表示的数是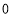 ,那么点
,那么点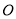 是(
是(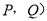 的( )
的( )
A.巧点 B. 妙点 C. 无法确定
(2)如图 2,
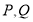 为数轴上两点,点
为数轴上两点,点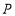 所表示的数为
所表示的数为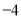 ,点
,点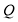 所表示的数为
所表示的数为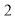 ,则(
,则(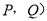 的巧点表示的数是 ;
的巧点表示的数是 ;

拓展提升
(3)如图 3,
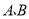 为数轴上两点,点
为数轴上两点,点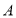 所表示的数为
所表示的数为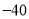 ,点
,点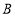 所表示的数为
所表示的数为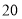 .现有一只电子蚂蚁P从点
.现有一只电子蚂蚁P从点  出发,以每
出发,以每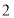 秒单位的速度向右运动,到达点
秒单位的速度向右运动,到达点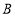 停止. 当经过几秒时,
停止. 当经过几秒时,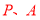 和
和 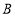 其有一个点为其余两点的巧点? (请直接写出结果)
其有一个点为其余两点的巧点? (请直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,一次函数y=kx﹣6(k≠0)的图象与y轴交于点A,与反比例函数y=
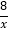 (x>0)的图象交于点B(4,b).
(x>0)的图象交于点B(4,b).(1)b= ;k= ;
(2)点C是线段AB上一点,过点C且平行于y轴的直线l交该反比例函数的图象于点D,连接OC,OD,BD,若四边形OCBD的面积S四边形OCBD=
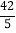 ,求点C的坐标;
,求点C的坐标;(3)将第(2)小题中的△OCD沿射线AB方向平移一定的距离后,得到△O'C'D',若点O的对应点O'恰好落在该反比例函数图象上(如图2),求此时点D的对应点D'的坐标.
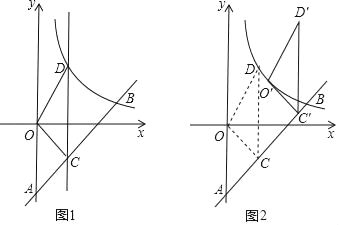
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,有一个数字迷宫,﹣2在迷宫的第一个拐角,3在第2个拐角,5在第3个拐角,7在第4个拐角,…那么第101个拐角是_____.
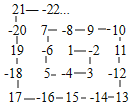
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣8)﹣(﹣15)+(﹣9)﹣(﹣12)
(2)7
 +(﹣6.5)+3
+(﹣6.5)+3 +(﹣1.25)+2
+(﹣1.25)+2
(3)(﹣81)÷(﹣2
 )×
)× ÷(﹣8)
÷(﹣8)(4)
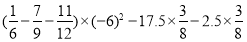
(5)
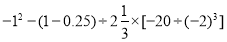
(6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:若在一个两位正整数N的个位数字与十位数字之间添上数字6,组成一个新的三位数,我们称这个三位数为N的“至善数”,如34的“至善数为364”;若将一个两位正整数M加6后得到一个新数,我们称这个新数为M的“明德数”,如34的“明德数为40”.
(1)30的“至善数”是 ,“明德数”是 .
(2)求证:对任意一个两位正整数A,其“至善数”与“明德数”之差能被9整除;
(3)若一个两位正整数B的明德数的各位数字之和是B的至善数各位数字之和的一半,求B的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
相关试题

