搜索
【题目】如图，在四边形ABCD中，AD=BC，∠A=∠B，E为AB的中点，连结CE，DE.
（1）求证：△ADE≌△BCE.
（2）若∠A＝70°，∠BCE＝60°，求∠CDE的度数．
参考答案：
【答案】（1）证明见解析；（2）50°.
【解析】
（1）由E为AB中点可得AE=BE，根据AD=BC，∠A=∠B，利用SAS即可证明△ADE≌△BCE；（2）由（1）得△ADE≌△BCE，可得DE=EC，∠ADE=∠BCE=60°，根据三角形内角和定理可得∠AED=∠BEC=50°，根据平角定义可得∠DEC的度数，根据等腰三角形的性质即可求出∠CDE的度数.
（1）∵E为AB的中点，
∴AE=BE，
又∵AD=BC，∠A=∠B，
∴△ADE≌△BCE；
（2）由（1）得△ADE≌△BCE，
∴DE=EC，∠ADE=∠BCE=60°，∠AED=∠BEC，
∵∠A=∠B=70°，
∴∠AED=∠BEC=180°-60°-70°=50°，
∴∠DEC=180°-50°-50°=80°，
∵DE=EC，
∴∠CDE=
(180°-80°)=50°
-
科目： 来源： 题型：
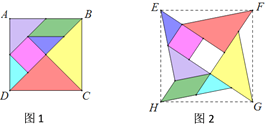
查看答案和解析>>【题目】七巧板是我们祖先的一项卓越创造，被西方人誉为“东方魔板”．下面的两幅图正方形（如图1）、“风车型”（如图2）都是由同一副七巧板拼成的，则图中正方形ABCD，EFGH的面积比为______.
-
科目： 来源： 题型：
查看答案和解析>>【题目】对非负实数x“四舍五入”到个位的值记为< x >，即已知n为正整数，如果n－
≤x＜n＋，那么< x >＝n．例如：< 0 >＝< 0.48 >＝0，< 0.64 >＝< 1.493 >＝1，< 2 >＝2，< 3.5 >＝< 4.12 >＝4，…则满足方程< x >＝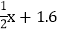
的非负实数x的值为____. -
科目： 来源： 题型：
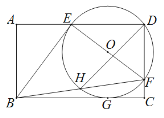
查看答案和解析>>【题目】如图，矩形ABCD中，点E，F分别在边AD，CD上，且EF⊥BE，EF=BE，△DEF的外接圆⊙O恰好切BC于点G，BF交⊙O于点H，连结DH.若AB=8，则DH=_____.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司销售部有营业员16人，销售部为了制定某种商品的月销售定额，统计了这16人某月的销售量如下：
每人销售件数
10
11
12
13
14
15
人数
1
3
4
3
3
2
（1）这16位销售员该月销售量的众数是_____，中位数是_____,平均数是_____.
（2）若要使75%的营业员都能完成任务，应选什么统计量（平均数、中位数和众数）作为月销售件数的定额？请说明理由.
-
科目： 来源： 题型：
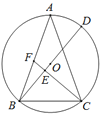
查看答案和解析>>【题目】如图，△ABC内接于⊙O，AB=AC，CF垂直直径BD于点E，交边AB于点F.
（1）求证：∠BFC=∠ABC.
（2）若⊙O的半径为5，CF=6，求AF长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某茶叶销售商计划将m罐茶叶按甲、乙两种礼品盒包装出售，其中甲种礼品盒每盒装4罐，每盒售价240元；乙种礼品盒每盒装6罐，每盒售价300元，恰好全部装完.已知每罐茶叶的成本价为30元，设甲种礼品盒的数量为x盒，乙种礼品盒的数量为y盒.
(1)当m=120时.
①求y关于x的函数关系式.
②若120罐茶叶全部售出后的总利润不低于3000元，则甲种礼品盒的数量至少要多少盒？
(2)若m罐茶叶全部售出后平均每罐的利润恰好为24元，且甲、乙两种礼品盒的数量和不超过69盒，求m的最大值.
相关试题
