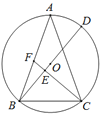
【题目】如图,△ABC内接于⊙O,AB=AC,CF垂直直径BD于点E,交边AB于点F.
(1)求证:∠BFC=∠ABC.
(2)若⊙O的半径为5,CF=6,求AF长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连结AD,由BD是直径可得∠BAD=90°,由CF⊥BD可得∠BEF=90°,可得∠BFC=∠ADB,根据等腰三角形性质和圆周角定理即可证明∠BFC=∠ABC;(2)连接CD,由BD是直径可得∠BCD=90°,根据(1)的结论可得CF=BC=6,利用勾股定理可求出CD的长,即可得∠DBC的余弦和正弦值,进而可得CE、BE的长,即可得EF的长,利用勾股定理可得BF的长,即可求出![]() 的余弦值,进而求出AB的长,根据AF=AB-BF即可得答案.
的余弦值,进而求出AB的长,根据AF=AB-BF即可得答案.
(1)证明:连结AD,
∵BD是⊙O的直径,
∴∠BAD=90°,
∵CF⊥BD,
∴∠BEF =90°,
∵∠ABD+∠ADB=90°,∠ABD+∠BFE=90°,
∴∠BFC=∠ADB,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ACB=∠ADB,
∴∠BFC=∠ABC.
(2)连结CD,
∵BD是⊙O的直径,
∴∠BCD=90°,
∵∠BFC=∠ABC,
∴BC=CF=6,
∵BD=10,
∴CD=![]() =8,
=8,
∴cos∠DBC=![]() ,sin∠DBC=
,sin∠DBC=![]() ,
,
在Rt△BCE中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,即
,即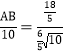 ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
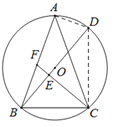
查看答案和解析>>【题目】如图,矩形ABCD中,点E,F分别在边AD,CD上,且EF⊥BE,EF=BE,△DEF的外接圆⊙O恰好切BC于点G,BF交⊙O于点H,连结DH.若AB=8,则DH=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD=BC,∠A=∠B,E为AB的中点,连结CE,DE.
(1)求证:△ADE≌△BCE.
(2)若∠A=70°,∠BCE=60°,求∠CDE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售部有营业员16人,销售部为了制定某种商品的月销售定额,统计了这16人某月的销售量如下:
每人销售件数
10
11
12
13
14
15
人数
1
3
4
3
3
2
(1)这16位销售员该月销售量的众数是_____,中位数是_____,平均数是_____.
(2)若要使75%的营业员都能完成任务,应选什么统计量(平均数、中位数和众数)作为月销售件数的定额?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某茶叶销售商计划将m罐茶叶按甲、乙两种礼品盒包装出售,其中甲种礼品盒每盒装4罐,每盒售价240元;乙种礼品盒每盒装6罐,每盒售价300元,恰好全部装完.已知每罐茶叶的成本价为30元,设甲种礼品盒的数量为x盒,乙种礼品盒的数量为y盒.
(1)当m=120时.
①求y关于x的函数关系式.
②若120罐茶叶全部售出后的总利润不低于3000元,则甲种礼品盒的数量至少要多少盒?
(2)若m罐茶叶全部售出后平均每罐的利润恰好为24元,且甲、乙两种礼品盒的数量和不超过69盒,求m的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,抛物线y=a( x-4 )2-16(a>0)交x轴于点E,F(E在F的左边),交y轴于点C,对称轴MN交x轴于点H;直线y=
 x+b分别交x,y轴于点A,B.
x+b分别交x,y轴于点A,B.(1)写出该抛物线顶点D的坐标及点C的纵坐标(用含a的代数式表示).
(2)若AF=AH=OH,求证:∠CEO=∠ABO.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,直线
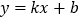 分别交x,y轴于点A(-8,0),B(0,6),C(m,0)是射线AO上一动点,⊙P过B,O,C三点,交直线AB于点D(B,D不重合).
分别交x,y轴于点A(-8,0),B(0,6),C(m,0)是射线AO上一动点,⊙P过B,O,C三点,交直线AB于点D(B,D不重合).(1)求直线AB的函数表达式.
(2)若点D在第一象限,且tan∠ODC=
 ,求点D的坐标.
,求点D的坐标.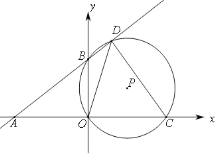
相关试题

