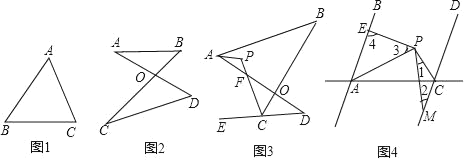
【题目】(1)如图,请证明∠A+∠B+∠C=180°
(2)如图的图形我们把它称为“8字形”,请证明∠A+∠B=∠C+∠D
(3)如图,E在DC的延长线上,AP平分∠BAD,CP平分∠BCE,猜想∠P与∠B、∠D之间的关系,并证明
(4)如图,AB∥CD,PA平分∠BAC,PC平分∠ACD,过点P作PM、PE交CD于M,交AB于E,则①∠1+∠2+∠3+∠4不变;②∠3+∠4﹣∠1﹣∠2不变,选择正确的并给予证明.
参考答案:
【答案】(1)见解析;(2)见解析;(3)∠P=90°+![]() (∠B+∠D);(4)∠3+∠4﹣∠1﹣∠2不变正确.理由见解析
(∠B+∠D);(4)∠3+∠4﹣∠1﹣∠2不变正确.理由见解析
【解析】
(1)延长BC到D,过点C作CE∥BA,根据两直线平行,同位角相等可得∠B=∠1,两直线平行,内错角相等可得∠A=∠2,再根据平角的定义列式整理即可得证;
(2)根据三角形内角和定理即可证明;
(3)根据(2)的结论∠B+∠BAD=∠D+∠BCD,∠PAD+∠P=∠D+∠PCD,然后整理即可得解;
(4)作PQ∥AB,根据平行线性质得到PQ∥CD,则∠APQ=180°﹣∠3﹣∠4,∠5=∠2,由于∠APQ+∠5+∠1=90°,则180°﹣∠3﹣∠4+∠2+∠1=90°,整理得到∠3+∠4﹣∠1﹣∠2=90°.
(1)证明:如图1,延长BC到D,过点C作CE∥BA,
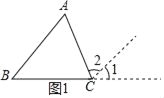
∵BA∥CE,
∴∠B=∠1,
∠A=∠2,
又∵∠BCD=∠BCA+∠2+∠1=180°,
∴∠A+∠B+∠ACB=180°;
(2)证明:如图2,在△AOB中,∠A+∠B+∠AOB=180°,

在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(3)如图3,
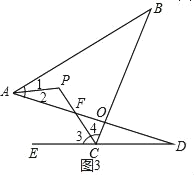
∵AP平分∠BAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∵(∠1+∠2)+∠B=(180°﹣2∠3)+∠D,
∠2+∠P=(180°﹣∠3)+∠D,
∴2∠P=180°+∠D+∠B,
∴∠P=90°+![]() (∠B+∠D);
(∠B+∠D);
(4)②∠3+∠4﹣∠1﹣∠2不变正确.
理由如下:
作PQ∥AB,如图4,
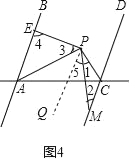
∵AB∥CD,
∴PQ∥CD,
由AB∥PQ得∠APQ+∠3+∠4=180°,即∠APQ=180°﹣∠3﹣∠4,
由PQ∥CD得∠5=∠2,
∵∠APQ+∠5+∠1=90°,
∴180°﹣∠3﹣∠4+∠2+∠1=90°,
∴∠3+∠4﹣∠1﹣∠2=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当3CQ=CE时,EP+BP= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
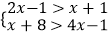 ,并把解集在如图数轴上表示出来.
,并把解集在如图数轴上表示出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,延长BC到点F,连接AF,使∠ABC=2∠CAF.
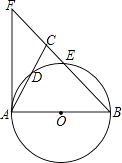
(1)求证:AF是⊙O的切线;
(2)若AC=4,CE:EB=1:3,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车
乙种客车
载客量(座/辆)
60
45
租金(元/辆)
550
450
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,CE⊥AB 于 E,DF⊥AB 于 F,AC∥ED,CE 是∠ACB 的平分线, 则图中与∠FDB 相等的角(不包含∠FDB)的个数为( )

A. 3 B. 4 C. 5 D. 6
相关试题

