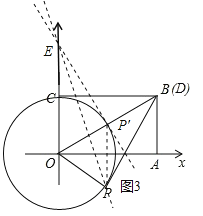
【题目】如图,矩形 ![]() 中,点
中,点 ![]() ,点
,点 ![]() 分别在
分别在 ![]() 轴,
轴,![]() 轴上,
轴上,![]() 为边
为边 ![]() 上的一动点,现把
上的一动点,现把 ![]() 沿
沿 ![]() 对折,
对折,![]() 点落在点
点落在点 ![]() 处.已知点
处.已知点 ![]() 的坐标为
的坐标为 ![]() .
.

(1) 当 ![]() 点坐标为
点坐标为 ![]() 时,求
时,求 ![]() 点的坐标;
点的坐标;
(2) 在点 ![]() 沿
沿 ![]() 从点
从点 ![]() 运动至点
运动至点 ![]() 的过程中,设点
的过程中,设点 ![]() 经过的路径长度为
经过的路径长度为 ![]() ,求
,求 ![]() 的值;
的值;
(3) 在点 ![]() 沿
沿 ![]() 从点
从点 ![]() 运动至点
运动至点 ![]() 的过程中,若点
的过程中,若点 ![]() 落在同一条直线
落在同一条直线 ![]() 上的次数为
上的次数为 ![]() 次,请直接写出
次,请直接写出 ![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)点 ![]() 的坐标为
的坐标为 ![]() ;(2)
;(2)![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:(1)依据题意画出图形,根据点D的坐标结合矩形的性质得出四边形OCDP是正方形,由此可得P点坐标,(2)由OP的长度为定值,可知点P的运动轨迹为以2为半径的圆弧,结合点B的坐标借助于特殊角的三角函数值得出∠COP=120°,再套用弧长公式即可得出结论,(3)取点E(0,4),过点E作圆O(弧CP段)的切线EP’,连接PP’,找出点P,P’的坐标,利用待定系数法求出k的值,再结合图形即可得出结论.
试题解析:(1)如图1,当D点坐标为(2,2)时,CD=2,因为OC=2,且四边形OABC为矩形,四边形OCDP是正方形,所以OP=2,所以点P的坐标为(2,0),

(2)如图2,因为在运动过程中,OP=OC始终成立,所以OP=2为定长,所以点P在以点O为圆心,以2为半径的圆上,因为点B的坐标为(![]() ,2),所以tan∠COB=
,2),所以tan∠COB=![]() ,
,
所以∠COB=60°,∠COP=120°,所以弧长=![]() ,
,

(3)在图2的基础上,取点E(0,4),过点E作圆O(弧CP段)的切线EP’,切点为P’,连接PP’,因为OE=4,OP’=2,所以sin∠OEP’=![]() ,所以∠OEP’=30°,所以∠EOP’=60°,
,所以∠OEP’=30°,所以∠EOP’=60°,
因为∠COP=120°,所以∠POP’=60°,因为OP=OP’,所以三角形OPP’为等边三角形,
因为OP=2,所以P(![]() ),P’(
),P’(![]() ),
),
当点P在直线y=kx+4上时,有-1=![]() ,所以k=
,所以k=![]() ,
,
当点P’在y=kx+4上时,有1=![]() ,所以k=
,所以k=![]() ,
,
综合可得:若点P落在同一条直线y=kx+4上的次数为2次,则k的取值范围为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线
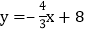 与
与  轴、
轴、  轴分别交于点
轴分别交于点 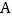 和点
和点 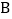 ,
,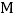 是
是  上的一点,若将
上的一点,若将 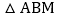 沿
沿  折叠,点
折叠,点 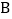 恰好落在
恰好落在 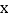 轴上的点
轴上的点 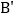 处,则直线
处,则直线  的解析式为________________.
的解析式为________________.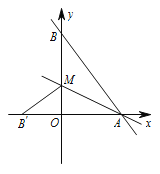
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明上周零花钱使用情况:(规定:超过50元记为正,少于50元记为负)
星期一
星期二
星期三
星期四
星期五
+11
+10
﹣17
+18
﹣12
请你解答以下问题:
(1)上星期五小明用了多少零花钱;
(2)上星期四比上星期三多花了多少零花钱;
(3)求上周平均每天用多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
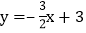 的图象与
的图象与 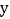 、
、 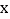 轴分别交于点
轴分别交于点 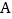 、
、 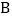 ,直线
,直线 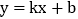 经过
经过 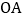 上的三分之一点
上的三分之一点 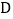 ,且交
,且交 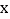 轴的负半轴于点
轴的负半轴于点 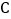 ,如果
,如果 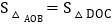 ,求直线
,求直线 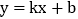 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,已知温沪动车铁路上有A、B、C三站,B、C两地相距
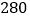 千米,甲、乙两列动车分别从B、C两地同时沿铁路匀速相向出发向终点C、B站而行,甲、乙两动车离A地的距离
千米,甲、乙两列动车分别从B、C两地同时沿铁路匀速相向出发向终点C、B站而行,甲、乙两动车离A地的距离  (千米)与行驶时间表
(千米)与行驶时间表  (时)的关系如图2所示,根据图象,解答以下问题:
(时)的关系如图2所示,根据图象,解答以下问题: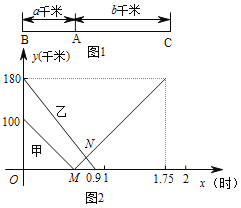
(1) 填空:路程
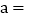 ________________,路程
________________,路程 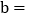 ________________,点
________________,点 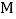 的坐标为________________.
的坐标为________________.(2) 求动车甲离A地的距离
 与行驶时间
与行驶时间 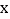 之间的函数关系式.
之间的函数关系式.(3) 补全动车乙的大致的函数图象.(直接画出图象)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将半径为2,圆心角为
 的扇形OAB绕点A逆时针旋转
的扇形OAB绕点A逆时针旋转 ,点
,点 的对应点分别为
的对应点分别为 ,连接
,连接 ,则图中阴影部分的面积是
,则图中阴影部分的面积是

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知张强家、体育场、文具店在同一直线上,下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中
 表示时间,
表示时间, 表示张强离家的距离.
表示张强离家的距离.
根据图象解答下列问题:
(1)体育场离张强家多远?张强从家到体育场用了多少时间?
(2)体育场离文具店多远?
(3)张强在文具店停留了多少时间?
(4)求张强从文具店回家过程中
 与
与 的函数解析式.
的函数解析式.
相关试题

