搜索
【题目】如图，在
和
中，
与
相交于
，
，
．
（1）求证：
；
（2）请用无刻度的直尺在下图中作出
的中点
．
参考答案：
【答案】（1）证明见解析；（2）见解析．
【解析】
（1）由SAS证明△DAB≌△CBA，得出对应角相等∠DBA=∠CAB，再由等角对等边即可得出结论；
（2）延长AD和BC相交于点F，作射线FE交AB于点M，根据轴对称的性质可证得点M就是所求作的中点．
（1）在△ABC和≌△BAD中，
∵
，
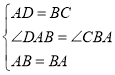∴△ABC≌△BAD，
∴∠DBA=∠CAB，
∴AE=BE；
（2）如图，点M就是所求作的中点．
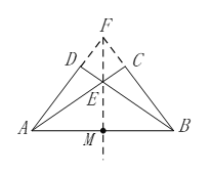
理由是：
由（1）可知：△ABC≌△BAD，
∴∠DBA=∠CAB，∠DAB=∠CBA，
∴EA=EB，FA=FB，
∴点A、B关于直线FE对称，
∴点M就是线段AB的中点．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市正在举行文化艺术节活动，一商店抓住商机，决定购进甲，乙两种艺术节纪念品．若购进甲种纪念品4件，乙种纪念品3件，需要550元，若购进甲种纪念品5件，乙种纪念品6件，需要800元．
（1）求购进甲、乙两种纪念品每件各需多少元？
（2）若该商店决定购进这两种纪念品共80件，其中甲种纪念品的数量不少于60件．考虑到资金周转，用于购买这80件纪念品的资金不能超过7100元，那么该商店共有几种进货方案7
（3）若销售每件甲种纪含晶可获利润20元，每件乙种纪念品可获利润30元．在（2）中的各种进货方案中，若全部销售完，哪一种方案获利最大？最大利利润多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）问题发现
如图1，在Rt△ABC中，∠A=90°，
=1，点P是边BC上一动点（不与点B重合），∠PAD=90°，∠APD=∠B，连接 CD．（1）①求
的值；②求∠ACD的度数．（2）拓展探究
如图 2，在Rt△ABC中，∠A=90°，
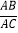=k．点P是边BC上一动点（不与点B重合），∠PAD=90°，∠APD=∠B，连接CD，请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系，并说明理由．（3）解决问题
如图 3，在△ABC中，∠B=45°，AB=4
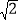，BC=12，P 是边BC上一动点（不与点B重合），∠PAD=∠BAC，∠APD=∠B，连接CD．若 PA=5，请直接写出CD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2﹣2ax+c（a≠0）与y轴交于点C（0，4），与x轴交于点A、B，点A坐标为（4，0）．
（1）求该抛物线的解析式；
（2）抛物线的顶点为N，在x轴上找一点K，使CK+KN最小，并求出点K的坐标；
（3）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ．当△CQE的面积最大时，求点Q的坐标；
（4）若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）．问：是否存在这样的直线l，使得△ODF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．
-
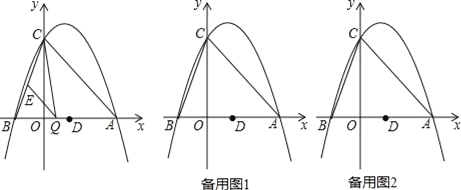
科目： 来源： 题型：
查看答案和解析>>【题目】列方程解应用题：
港珠澳大桥是世界上最长的跨海大桥，是被誉为“现代世界七大奇迹”的超级工程，它是我国从桥梁大国走向桥梁强国的里程碑之作．开通后从香港到珠海的车程由原来的180千米缩短到50千米，港珠澳大桥的设计时速比按原来路程行驶的平均时速多40千米，若开通后按设计时速行驶，行驶完全程时间仅为原来路程行驶完全程时间的
，求港珠澳大桥的设计时速是多少． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知⊙O的半径为10，圆心O到弦AB的距离为5，则弦AB所对的圆周角的度数是（ ）
A. 30° B. 60° C. 30°或150° D. 60°或120°
-
科目： 来源： 题型：
查看答案和解析>>【题目】“综合与实践”学习活动准备制作一组三角形，记这些三角形的三边分别为
，
，
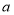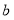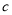，用记号
表示一个满足条件的三角形，如
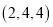表示边长分别为2，4，4个单位长度的一个三角形．（1）若这些三角形三边的长度为大于0且小于3的整数个单位长度，请用记号写出所有满足条件的三角形；
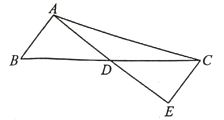
（2）如图，
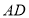是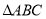
的中线，线段
，
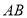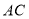的长度分别为2个，6个单位长度，且线段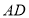的长度为整数个单位长度，过点
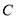作
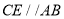交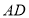的延长线于点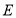
①求
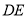之长；②请直接用记号表示
．
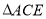相关试题
