【题目】如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A坐标为(4,0).
(1)求该抛物线的解析式;
(2)抛物线的顶点为N,在x轴上找一点K,使CK+KN最小,并求出点K的坐标;
(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(4)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线解析式为y=﹣![]() x2+x+4;(2)点K的坐标为(
x2+x+4;(2)点K的坐标为(![]() ,0);(3)当m=1时,S△CQE有最大值3,此时Q(1,0);(4)存在这样的直线l,使得△ODF是等腰三角形.所求点P的坐标为:(1+
,0);(3)当m=1时,S△CQE有最大值3,此时Q(1,0);(4)存在这样的直线l,使得△ODF是等腰三角形.所求点P的坐标为:(1+![]() ,2)或(1﹣
,2)或(1﹣![]() ,2)或(1+
,2)或(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3).
,3).
【解析】试题分析:(1)把A、C两点坐标代入抛物线解析式可求得a、c的值,可求得抛物线解析;
(2)可求得点C关于x轴的对称点C′的坐标,连接C′N交x轴于点K,再求得直线C′K的解析式,可求得K点坐标;
(3)过点E作EG⊥x轴于点G,设Q(m,0),可表示出AB、BQ,再证明△BQE≌△BAC,可表示出EG,可得出△CQE关于m的解析式,再根据二次函数的性质可求得Q点的坐标;
(4)分DO=DF、FO=FD和OD=OF三种情况,分别根据等腰三角形的性质求得F点的坐标,进一步求得P点坐标即可.
试题解析:(1)∵抛物线经过点C(0,4),A(4,0),
∴![]() ,解得
,解得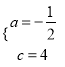 ,
,
∴抛物线解析式为y=﹣![]() x2+x+4;
x2+x+4;
(2)由(1)可求得抛物线顶点为N(1, ![]() ),
),
如图1,作点C关于x轴的对称点C′(0,﹣4),连接C′N交x轴于点K,则K点即为所求,
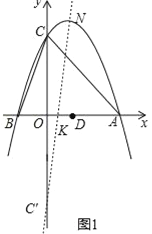
设直线C′N的解析式为y=kx+b,把C′、N点坐标代入可得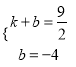 ,解得
,解得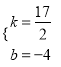 ,
,
∴直线C′N的解析式为y=![]() x-4 ,
x-4 ,
令y=0,解得x=![]() ,
,
∴点K的坐标为(![]() ,0);
,0);
(3)设点Q(m,0),过点E作EG⊥x轴于点G,如图2,
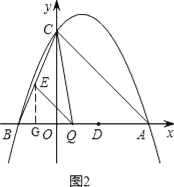
由﹣![]() x2+x+4=0,得x1=﹣2,x2=4,
x2+x+4=0,得x1=﹣2,x2=4,
∴点B的坐标为(﹣2,0),AB=6,BQ=m+2,
又∵QE∥AC,∴△BQE≌△BAC,
∴![]() ,即
,即![]() ,解得EG=
,解得EG=![]() ;
;
∴S△CQE=S△CBQ﹣S△EBQ=![]() (CO-EG)·BQ=
(CO-EG)·BQ=![]() (m+2)(4-
(m+2)(4-![]() )
)
=![]() =-
=-![]() (m-1)2+3 .
(m-1)2+3 .
又∵﹣2≤m≤4,
∴当m=1时,S△CQE有最大值3,此时Q(1,0);
(4)存在.在△ODF中,
(ⅰ)若DO=DF,∵A(4,0),D(2,0),
∴AD=OD=DF=2.
又在Rt△AOC中,OA=OC=4,
∴∠OAC=45°.
∴∠DFA=∠OAC=45°.
∴∠ADF=90°.
此时,点F的坐标为(2,2).
由﹣![]() x2+x+4=2,得x1=1+
x2+x+4=2,得x1=1+![]() ,x2=1﹣
,x2=1﹣![]() .
.
此时,点P的坐标为:P1(1+![]() ,2)或P2(1﹣
,2)或P2(1﹣![]() ,2);
,2);
(ⅱ)若FO=FD,过点F作FM⊥x轴于点M.
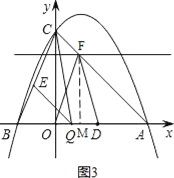
由等腰三角形的性质得:OM=![]() OD=1,
OD=1,
∴AM=3.
∴在等腰直角△AMF中,MF=AM=3.
∴F(1,3).
由﹣![]() x2+x+4=3,得x1=1+
x2+x+4=3,得x1=1+![]() ,x2=1﹣
,x2=1﹣![]() .
.
此时,点P的坐标为:P3(1+![]() ,3)或P4(1﹣
,3)或P4(1﹣![]() ,3);
,3);
(ⅲ)若OD=OF,
∵OA=OC=4,且∠AOC=90°.
∴AC=4![]() .
.
∴点O到AC的距离为2![]() .
.
而OF=OD=2<2![]() ,与OF≥2
,与OF≥2![]() 矛盾.
矛盾.
∴在AC上不存在点使得OF=OD=2.
此时,不存在这样的直线l,使得△ODF是等腰三角形.
综上所述,存在这样的直线l,使得△ODF是等腰三角形.所求点P的坐标为:(1+![]() ,2)或(1﹣
,2)或(1﹣![]() ,2)或(1+
,2)或(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3).
,3).
-
科目: 来源: 题型:
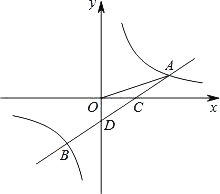
查看答案和解析>>【题目】如图,一次函数y=ax﹣1的图象与反比例函数y=
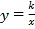 的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=
的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA= ,tan∠AOC=
,tan∠AOC= .
.(1)求a,k的值及点B的坐标;
(2)观察图象,请直接写出不等式ax﹣1≥
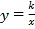 的解集;
的解集;(3)在y轴上存在一点P,使得△PDC与△ODC相似,请你求出P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市正在举行文化艺术节活动,一商店抓住商机,决定购进甲,乙两种艺术节纪念品.若购进甲种纪念品4件,乙种纪念品3件,需要550元,若购进甲种纪念品5件,乙种纪念品6件,需要800元.
(1)求购进甲、乙两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共80件,其中甲种纪念品的数量不少于60件.考虑到资金周转,用于购买这80件纪念品的资金不能超过7100元,那么该商店共有几种进货方案7
(3)若销售每件甲种纪含晶可获利润20元,每件乙种纪念品可获利润30元.在(2)中的各种进货方案中,若全部销售完,哪一种方案获利最大?最大利利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现
如图1,在Rt△ABC中,∠A=90°,
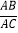 =1,点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接 CD.
=1,点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接 CD.(1)①求
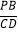 的值;②求∠ACD的度数.
的值;②求∠ACD的度数.(2)拓展探究
如图 2,在Rt△ABC中,∠A=90°,
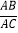 =k.点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接CD,请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系,并说明理由.
=k.点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接CD,请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系,并说明理由.(3)解决问题
如图 3,在△ABC中,∠B=45°,AB=4
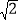 ,BC=12,P 是边BC上一动点(不与点B重合),∠PAD=∠BAC,∠APD=∠B,连接CD.若 PA=5,请直接写出CD的长.
,BC=12,P 是边BC上一动点(不与点B重合),∠PAD=∠BAC,∠APD=∠B,连接CD.若 PA=5,请直接写出CD的长.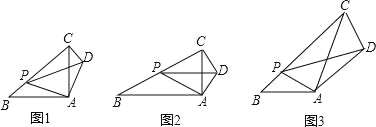
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 和
和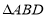 中,
中,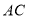 与
与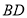 相交于
相交于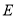 ,
,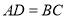 ,
,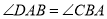 .
.
(1)求证:
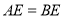 ;
;(2)请用无刻度的直尺在下图中作出
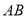 的中点
的中点 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
港珠澳大桥是世界上最长的跨海大桥,是被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.开通后从香港到珠海的车程由原来的180千米缩短到50千米,港珠澳大桥的设计时速比按原来路程行驶的平均时速多40千米,若开通后按设计时速行驶,行驶完全程时间仅为原来路程行驶完全程时间的
 ,求港珠澳大桥的设计时速是多少.
,求港珠澳大桥的设计时速是多少. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
相关试题

