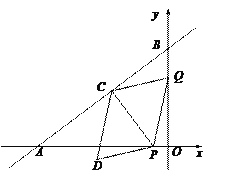
【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(-4,0),B(0,3),动点P从点O出发,沿x轴负方向以每秒1个单位的速度运动,同时动点Q从点B出发,沿射线BO方向以每秒2个单位的速度运动,过点P作PC⊥AB于点C,连接PQ,CQ,以PQ,CQ为邻边构造平行四边形PQCD,设点P运动的时间为t秒.
(1)当点Q在线段OB上时,用含t的代数式表示PC,AC的长;
(2)在运动过程中.
①当点D落在x轴上时,求出满足条件的t的值;
②若点D落在△ABO内部(不包括边界)时,直接写出t的取值范围;
(3)作点Q关于x轴的对称点Q′,连接CQ′,在运动过程中,是否存在某时刻使过A,P,C三点的圆与△CQQ′三边中的一条边相切?若存在,请求出t的值;若不存在,请说明理由.
参考答案:
【答案】(1)AC=![]() (4-t)(2)①
(4-t)(2)①![]() 时,点D在x轴上,
时,点D在x轴上,![]() (3)
(3)![]() 或
或![]()
【解析】(1)利用三角函数sin∠OAB=![]() =
=![]() ,cos∠OAB=
,cos∠OAB=![]() =
=![]() ,列出关系式即可解决问题.
,列出关系式即可解决问题.
(2)①当D在x轴上时,如图2中,由QC∥OA,得![]() =
=![]() ,由此即可解决问题. ②当点D在AB上时,如图3中,由PQ∥AB,得
,由此即可解决问题. ②当点D在AB上时,如图3中,由PQ∥AB,得![]() =
=![]() ,求出时间t,求出①②两种情形时 的△POQ的面积即可解决问题.
,求出时间t,求出①②两种情形时 的△POQ的面积即可解决问题.
(3)如图4中,当QC与⊙M相切时,则QC⊥CM,首先证明QBQ=QC,作QN∠BC于N,根据cos∠ABO=![]() =
=![]() ,列出方程即可解决问题,当CQ/是⊙M切线时,方法类似.
,列出方程即可解决问题,当CQ/是⊙M切线时,方法类似.
解:(1)如图1中,
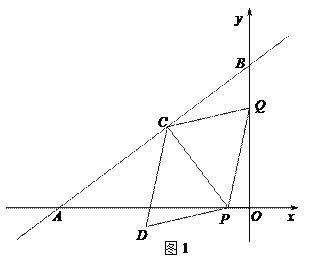
∵OA=8,OB=6,∴AB=![]() =5.
=5.
在Rt△ACP中,PA=4-t,
∵sin∠OAB=![]() ,∴PC=
,∴PC=![]() (4-t),
(4-t),
∵cos∠OAB=![]() ,∴AC=
,∴AC=![]() (4-t).
(4-t).
(2)①当D在x轴上时,如图2中,
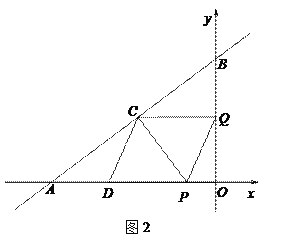
∵QC∥OA,∴![]() ∴
∴![]() ,
,
解得![]() .∴
.∴![]() 时,点D在x轴上.
时,点D在x轴上.
②![]() .
.
(3)如图3中,
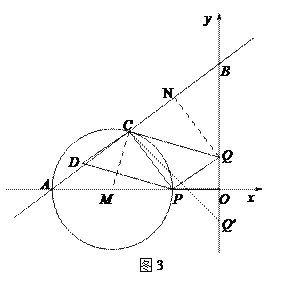
∵Q(0,3-2t),Q′(0,2t-3),
当QC与⊙M相切时,则QC⊥CM,
∴∠QCM=90°,∴∠QCP+∠PCM=90°,∵∠QCP+∠QCB=90°,
∴∠BCQ=∠PCM=∠CPM,
∵∠CPM+∠PAC=90°,∠OBA+∠OAB=90°,
∴∠APC=∠OBA,∴∠QBC=∠QCB,
∴BQ=CQ,作QN⊥BC于N,
∵cos∠ABO=![]() ,∴
,∴![]() ,
,
解得![]() ,
,
当CQ′是⊙M切线时,同理可得![]() ,解得
,解得![]() .
.
∴![]() 或
或![]() 时,过A,P,C三点的圆与△CQQ′三边中的一条边相切.
时,过A,P,C三点的圆与△CQQ′三边中的一条边相切.
“点睛”本题考查圆的综合题、锐角三角函数、四边形的性质、等腰三角形的性质、切线的性质等知识,解题的关键是求得点D在特殊位置时的时间,学会利用方程解决问题,属于中考压轴题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣125的立方根是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 (a为常数,且a>0)与x轴从左至右
(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线
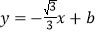 与抛物线的另一交
与抛物线的另一交点为D,且点D的横坐标为﹣5.
(1)求抛物线的函数表达式;
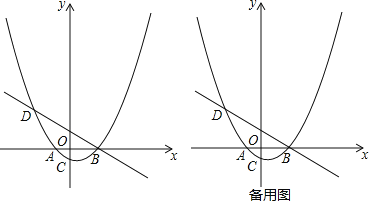
(2)P为直线BD下方的抛物线上的一点,连接PD、PB, 求△PBD面积的最大值.
(3)设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点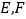 分别在正方形
分别在正方形 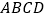 的边
的边 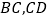 上,
上, 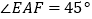 ,连接
,连接 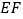 ,则
,则 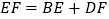 ,试说明理由.
,试说明理由.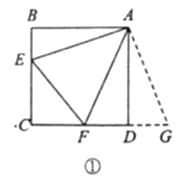
(1)思路梳理
因为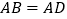 ,所以把
,所以把 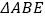 绕点
绕点 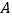 逆时针旋转90°至
逆时针旋转90°至 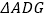 ,可使
,可使 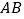 与
与 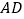 重合.因为
重合.因为 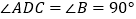 ,所以
,所以 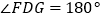 ,点
,点 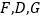 共线.
共线.
根据 , 易证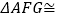 , 得
, 得 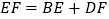 .请证明.
.请证明.
(2)类比引申
如图②,四边形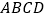 中,
中, 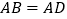 ,
, 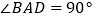 ,点
,点 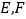 分别在边
分别在边 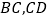 上,
上, 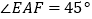 .若
.若 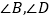 都不是直角,则当
都不是直角,则当 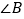 与
与  满足等量关系时,
满足等量关系时, 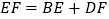 仍然成立,请证明.
仍然成立,请证明.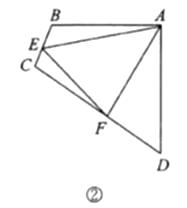
(3)联想拓展
如图③,在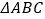 中,
中, 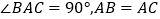 ,点
,点 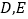 均在边
均在边 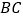 上,且
上,且 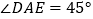 .猜想
.猜想 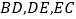 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.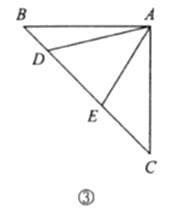
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组数为边长的三角形中,能组成直角三角形的是( )
A. 3,4,6 B. 15,20,25 C. 5,12,15 D. 10,16,25
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形具有而菱形不具有的性质是( )
A.两组对边分别平行
B.对角线相等
C.对角线互相平分
D.两组对角分别相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )
①△BDF≌△CDE;②CE=BF;③ABD和△ACD的面积相等;④BF∥CE.
A.1个
B.2个
C.3个
D.4个
相关试题

