【题目】已知关于x的一元二次方程mx2-(m+2)x+2=0(m≠0)
(1)求证:方程一定有两个实数根;
(2)若此方程的两根为不相等的整数,求整数m的值.
参考答案:
【答案】(1)见详解;(2)-1,-2,1
【解析】
(1)先计算判别式的值,然后根据判别式的意义即可得到方程总有两个不相等的实数根;
(2)利用求根公式法解方程得到x1=1,x2=![]() ,然后利用有理数的整除性确定m的值.
,然后利用有理数的整除性确定m的值.
(1)证明:∵一元二次方程mx2-(m+2)x+2=0(m≠0)
∴Δ=[-(m+2)] 2-4×2m=m2+4m+4-8m=(m-2)2,
∵m≠0
∴Δ=(m-2)2≥0
∴方程一定有两个实数根;
(2)解:由求根公式得,x1=1,x2=![]()
∵方程的两根为不相等的整数,且m为整数
∴![]() 是整数,而m≠0
是整数,而m≠0
∴m=±1,±2,
而当m=2时,x1=x2=1,(舍去)
∴整数m为1,-1,-2
故答案为:1,-1,-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=x+1与x、y 轴分别交于点A、B,在直线 AB上截取BB1=AB,过点B1分别作y 轴的垂线,垂足为点C1,得到⊿BB1C1;在直线 AB上截取B1B2= BB1,过点B2分别作y 轴的垂线,垂足为点C2,得到⊿BB2C2;在直线AB上截取B2B3= B1B2,过点B3作y 轴的垂线,垂足为点C3,得到⊿BB3C3;……;第3个⊿BB3C3的面积是___________;第n个⊿BBnCn的面积是______________(用含n的式子表示,n是正整数).
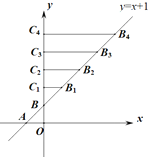
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发. 设两车离甲地的距离为
 ,两车行驶的时间为
,两车行驶的时间为 ,图中
,图中 分别表示两车离甲地的距离
分别表示两车离甲地的距离 与行驶时间
与行驶时间 之间的关系.
之间的关系.
(1)甲乙两地距离是多少?
(2)哪条线表示客车离甲地的距离
 与行驶时间
与行驶时间 之间的关系?
之间的关系?(3)请求出
 对应的两个一次函数的关系式;
对应的两个一次函数的关系式;(4)两车在行驶多长时间后相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(组),并将它的解集在数轴上表示出来.
(1)
 ; (2)
; (2) 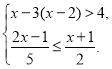
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,在平面直角坐标系中,点A,B,E分别是x轴和y轴上的任意点. BD是∠ABE的平分线,BD的反向延长线与∠OAB的平分线交于点C.
探究: (1)求∠C的度数.
发现: (2)当点A,点B分别在x轴和y轴的正半轴上移动时,∠C的大小是否发生变化?若不变,请直接写出结论;若发生变化,请求出∠C的变化范围.
应用:(3)如图2在五边形ABCDE中,∠A+∠B+∠E=310°,CF平分∠DCB,CF的反向延长线与∠EDC外角的平分线相交于点P,求∠P的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数

(1)在平面直角坐标系内画出该函数的图象;
(2)当自变量x=-4时,函数y的值_________;
(3)当x<0时,请结合图象,直接写出y的取值范围:_______.


-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知点
 、点
、点 ,一次函数
,一次函数 的图象与直线AB交于点P.
的图象与直线AB交于点P.(1)求直线AB的函数表达式及P点的坐标;
(2)若点Q是y轴上一点,且△BPQ的面积为2,求点Q的坐标.
相关试题

