【题目】已知:如图1,在平面直角坐标系中,点A,B,E分别是x轴和y轴上的任意点. BD是∠ABE的平分线,BD的反向延长线与∠OAB的平分线交于点C.
探究: (1)求∠C的度数.
发现: (2)当点A,点B分别在x轴和y轴的正半轴上移动时,∠C的大小是否发生变化?若不变,请直接写出结论;若发生变化,请求出∠C的变化范围.
应用:(3)如图2在五边形ABCDE中,∠A+∠B+∠E=310°,CF平分∠DCB,CF的反向延长线与∠EDC外角的平分线相交于点P,求∠P的度数.

参考答案:
【答案】(1)∠C=45°;(2)不变.∠C=![]() ∠AOB =45°; (3) 25°.
∠AOB =45°; (3) 25°.
【解析】
(1)先确定∠ABE与∠OAB的关系,∠ABE=∠OAB+90°,再根据角平分线和三角形的外角求得∠ACB的度数;
(2)设∠DBC=x,∠BAC=y,再根据BC平分∠DBO,AC平分∠BAO可知∠CBO=∠DBC=x,∠OAC=∠BAC=y.再由∠DBO是△AOB的外角,∠DBC是△ABC的外角可得出关于x、y,∠C的方程组,求出∠C的值即可;
(3)延长ED,BC相交于点G,易求∠G的度数,由三角形外角的性质可得结论.
(1)∵∠ABE=∠OAB+∠AOB,∠AOB =90°,
∴∠ABE=∠OAB+90°,
∵BD是∠ABE的平分线,AC平分∠OAB,
∴∠ABE=2∠ABD,∠OAB=2∠BAC,
∴2∠ABD=2∠BAC+90°,
∴∠ABD=∠BAC+45°,
又∵∠ABD= ∠BAC +∠C,
∴∠C=45°.
(2)不变.∠C=![]() ∠AOB =45°.
∠AOB =45°.
理由如下:
设∠DBA=x,∠BAC=y,
∵BD平分∠EBA,AC平分∠BAO.
∴∠EBD=∠DBA=x,∠OAC=∠BAC=y.
∵∠EBA是△AOB的外角,∠DBA是△ABC的外角,
∴![]() ,
,
∴∠C=45°.
(3) 延长ED,BC相交于点G.
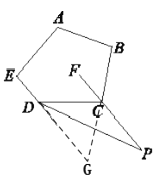
在四边形ABGE中,
∵∠G=360°-(∠A+∠B+∠E)=50°,
∴∠P=∠FCD-∠CDP=![]() (∠DCB-∠CDG)
(∠DCB-∠CDG)
=![]() ∠G=
∠G=![]() ×50°=25°.
×50°=25°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发. 设两车离甲地的距离为
 ,两车行驶的时间为
,两车行驶的时间为 ,图中
,图中 分别表示两车离甲地的距离
分别表示两车离甲地的距离 与行驶时间
与行驶时间 之间的关系.
之间的关系.
(1)甲乙两地距离是多少?
(2)哪条线表示客车离甲地的距离
 与行驶时间
与行驶时间 之间的关系?
之间的关系?(3)请求出
 对应的两个一次函数的关系式;
对应的两个一次函数的关系式;(4)两车在行驶多长时间后相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(组),并将它的解集在数轴上表示出来.
(1)
 ; (2)
; (2) 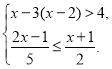
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程mx2-(m+2)x+2=0(m≠0)
(1)求证:方程一定有两个实数根;
(2)若此方程的两根为不相等的整数,求整数m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数

(1)在平面直角坐标系内画出该函数的图象;
(2)当自变量x=-4时,函数y的值_________;
(3)当x<0时,请结合图象,直接写出y的取值范围:_______.


-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知点
 、点
、点 ,一次函数
,一次函数 的图象与直线AB交于点P.
的图象与直线AB交于点P.(1)求直线AB的函数表达式及P点的坐标;
(2)若点Q是y轴上一点,且△BPQ的面积为2,求点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?

相关试题

