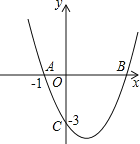
【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 两点,与x轴交于另一点B.
两点,与x轴交于另一点B.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 已知点
已知点![]() 在第四象限的抛物线上,求点D关于直线BC对称的点
在第四象限的抛物线上,求点D关于直线BC对称的点![]() 的坐标.
的坐标.
![]() 在
在![]() 的条件下,连接BD,问在x轴上是否存在点P,使
的条件下,连接BD,问在x轴上是否存在点P,使![]() ?若存在,请求出P点的坐标;若不存在,请说明理由.
?若存在,请求出P点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)点D关于直线BC对称的点
;(2)点D关于直线BC对称的点![]() ;
;![]() 存在,
存在,![]()
【解析】分析:(1)、将A(-1,0)、C(0,-3)两点坐标代入抛物线![]() 中,列方程组求a、b的值即可;(2)、将点D(m,-m-1)代入(1)中的抛物线解析式,求m的值,再根据对称性求点D关于直线BC对称的点D'的坐标;(3)、当∠PCB=∠CBD时,可知CP∥BD,根据三角形的全等关系确定P点坐标.
中,列方程组求a、b的值即可;(2)、将点D(m,-m-1)代入(1)中的抛物线解析式,求m的值,再根据对称性求点D关于直线BC对称的点D'的坐标;(3)、当∠PCB=∠CBD时,可知CP∥BD,根据三角形的全等关系确定P点坐标.
详解:![]() 将
将![]() 、
、![]() 代入抛物线
代入抛物线![]() 中,
中,
得![]() , 解得
, 解得![]() ,
, ![]() ;
;
![]() 将点
将点![]() 代入
代入![]() 中,得:
中,得:![]() ,
,
解得![]() 或
或![]() ,
, ![]() 点
点![]() 在第四象限,
在第四象限, ![]() ,
,
![]() 直线BC解析式为
直线BC解析式为![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
![]() 点D关于直线BC对称的点
点D关于直线BC对称的点![]() ;
;
![]() 存在
存在![]() 满足条件的点P有两个.
满足条件的点P有两个.
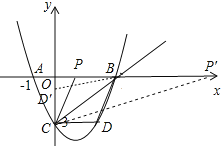
![]() 过点C作
过点C作![]() ,交x轴于P,则
,交x轴于P,则![]() ,
, ![]() 直线BD解析式为
直线BD解析式为![]() ,
,
![]() 直线CP过点C,
直线CP过点C, ![]() 直线CP的解析式为
直线CP的解析式为![]() ,
, ![]() 点P坐标
点P坐标![]() ,
,
![]() 连接
连接![]() ,过点C作
,过点C作![]() ,交x轴于
,交x轴于![]() ,
, ![]() ,
,
根据对称性可知![]() ,
, ![]() ,
, ![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
![]() 直线
直线![]() 过点C,
过点C, ![]() 直线
直线![]() 解析式为
解析式为![]() ,
, ![]() 坐标为
坐标为![]() ,
,
综上所述,满足条件的点P坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,这是网上盛传的一个关于数学的诡辩问题截图,表1是它的示意表.我们一起来解答“为什么多出了2元".

花去
剩余
买牛肉
40元
60元
买猪脚
30元
30元
买蔬菜
18元
12元
买调料
12元
0元
总计
100元
102元
表1
花去
剩余
买牛肉
40元
60元
买猪脚
30元
30元
买蔬菜
元
元
买调料
元
0元
总计
100元
103元
表2
花去
剩余
买物品1
a元
x元
买物品2
b元
y元
买物品3
c元
z元
买物品4
d元
0元
总计
100元
w元
表3
花去
剩余
买牛肉
元
元
买猪脚
元
元
买蔬菜
元
元
买调料
元
元
总计
元
/
表4
(1)为了解释“剩余金额总计”与“我手里有100元"无关,请按要求填写表2中的空格.
(2)如表3中,直接写出各代数式的值: .
①a+b+c+d=_ ;
②a+x=__ ;
③a+b+y=_ ;
④a+b+c+z=_ 。
(3)如表3中,a、b、c、d都是正整数,则w的最大值等于_ ,最小值等于_ ,由此可以知道“为什么多出了2元”只是一个诡辩而已.
(4)我们将“花去”记为“一”,“剩余”记为“+”,请在表4中将表1数据重新填写.
-
科目: 来源: 题型:
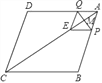
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为_____.
-
科目: 来源: 题型:
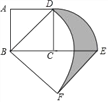
查看答案和解析>>【题目】如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接BF,则图中阴影部分的面积是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分剪下,拼成右边的矩形,由图形①到图形②的变化过程能够验证的一个等式是( )
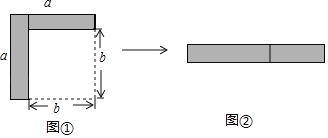
A. a(a+b)=a2+ab B. a2﹣b2=(a+b)(a﹣b)
C. (a+b)2=a2+2ab+b2 D. a(a﹣b)=a2﹣ab
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上顺次有
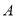 、
、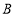 、
、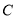 三点,分别表示数
三点,分别表示数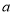 、
、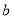 、
、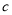 ,并且满足
,并且满足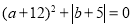 ,
,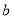 与
与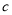 互为相反数.一只电子小蜗牛从
互为相反数.一只电子小蜗牛从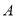 点向正方向移动,速度为2个单位/秒.
点向正方向移动,速度为2个单位/秒.(1)请求出
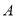 、
、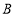 、
、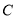 三点分别表示的数.
三点分别表示的数.(2)运动多少秒时,小蜗牛到点
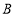 的距离为1个单位长度.
的距离为1个单位长度.(3)设点
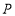 在数轴上点A的右边,且点
在数轴上点A的右边,且点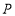 分别到点
分别到点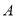 、点
、点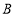 、点
、点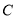 的距离之和是20,那么点
的距离之和是20,那么点 所表示的数是_____.
所表示的数是_____. -
科目: 来源: 题型:
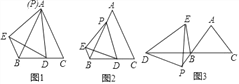
查看答案和解析>>【题目】已知,等边三角形ABC的边长为5,点P在线段AB上,点D在线段BC上,且△PDE是等边三角形.
(1)初步尝试:若点P与点A重合时(如图1),BD+BE= .
(2)类比探究:将点P沿AB方向移动,使AP=1,其余条件不变(如图2),试计算BD+BE的值是多少?
(3)拓展迁移:如图3,在△ABC中,AB=AC,∠BAC=70°,点P在线段AB的延长线上,点D在线段CB的延长线上,在△PDE中,PD=PE,∠DPE=70°,设BP=a,请直接写出线段BD、BE之间的数量关系(用含a的式子表示)
相关试题

