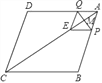
【题目】如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为_____.
参考答案:
【答案】![]() 或
或![]() .
.
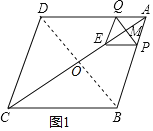
【解析】连接BD交AC于O,由四边形ABCD是菱形,得到AC⊥BD,推出△AMP∽△AOB,①当CE=CB时,如图1,则CE=10,AE=6,AM=3,根据相似三角形的性质得到![]() ,可求得AP=
,可求得AP=![]() ;
;
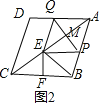
②当BE=EC时,如图2,点E是BC的垂直平分线与AC的交点,则CF=5,根据相似三角形的性质得到CE=![]() ,继而得出AE=16-
,继而得出AE=16-![]() =
=![]() ,然后可求出AM=
,然后可求出AM=![]() ,根据对应边的比求出AP=
,根据对应边的比求出AP=![]() ;
;
③当BC=BE时,E与A重合;
综上所述:当△BCE是等腰三角形时,AP的长为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
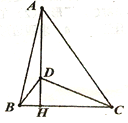
查看答案和解析>>【题目】如图在△ABC中,AH⊥BC于点H,在AH上取一点D,连接DC,使DA=DC,且∠ADC=2∠DBC,若DH=2,BC=6,则AB=_________________。
-
科目: 来源: 题型:
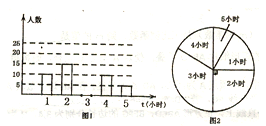
查看答案和解析>>【题目】为了解某校八年级学生每周平均课外阅读时间的情况,随机抽查了该校八年级部分学生,对其每周平均课外阅读时间进行统计,根据统计数据绘制成如图的两幅尚不完整的统计图:
(1)本次共抽取了多少人?并请将图1的条形图补充完整;
(2)这组数据的众数是________;求出这组数据的平均数;
(3)若全校有1500人,请你估计每周平均课外阅读时间为3小时的学生多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,这是网上盛传的一个关于数学的诡辩问题截图,表1是它的示意表.我们一起来解答“为什么多出了2元".

花去
剩余
买牛肉
40元
60元
买猪脚
30元
30元
买蔬菜
18元
12元
买调料
12元
0元
总计
100元
102元
表1
花去
剩余
买牛肉
40元
60元
买猪脚
30元
30元
买蔬菜
元
元
买调料
元
0元
总计
100元
103元
表2
花去
剩余
买物品1
a元
x元
买物品2
b元
y元
买物品3
c元
z元
买物品4
d元
0元
总计
100元
w元
表3
花去
剩余
买牛肉
元
元
买猪脚
元
元
买蔬菜
元
元
买调料
元
元
总计
元
/
表4
(1)为了解释“剩余金额总计”与“我手里有100元"无关,请按要求填写表2中的空格.
(2)如表3中,直接写出各代数式的值: .
①a+b+c+d=_ ;
②a+x=__ ;
③a+b+y=_ ;
④a+b+c+z=_ 。
(3)如表3中,a、b、c、d都是正整数,则w的最大值等于_ ,最小值等于_ ,由此可以知道“为什么多出了2元”只是一个诡辩而已.
(4)我们将“花去”记为“一”,“剩余”记为“+”,请在表4中将表1数据重新填写.
-
科目: 来源: 题型:
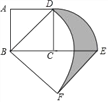
查看答案和解析>>【题目】如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接BF,则图中阴影部分的面积是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
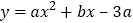 经过
经过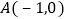 、
、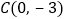 两点,与x轴交于另一点B.
两点,与x轴交于另一点B.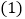 求此抛物线的解析式;
求此抛物线的解析式;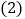 已知点
已知点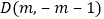 在第四象限的抛物线上,求点D关于直线BC对称的点
在第四象限的抛物线上,求点D关于直线BC对称的点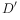 的坐标.
的坐标.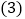 在
在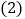 的条件下,连接BD,问在x轴上是否存在点P,使
的条件下,连接BD,问在x轴上是否存在点P,使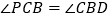 ?若存在,请求出P点的坐标;若不存在,请说明理由.
?若存在,请求出P点的坐标;若不存在,请说明理由.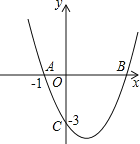
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分剪下,拼成右边的矩形,由图形①到图形②的变化过程能够验证的一个等式是( )
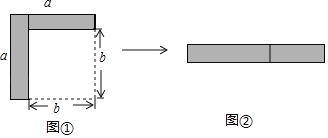
A. a(a+b)=a2+ab B. a2﹣b2=(a+b)(a﹣b)
C. (a+b)2=a2+2ab+b2 D. a(a﹣b)=a2﹣ab
相关试题

