【题目】已知,等边三角形ABC的边长为5,点P在线段AB上,点D在线段BC上,且△PDE是等边三角形.
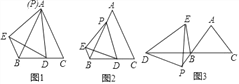
(1)初步尝试:若点P与点A重合时(如图1),BD+BE= .
(2)类比探究:将点P沿AB方向移动,使AP=1,其余条件不变(如图2),试计算BD+BE的值是多少?
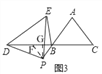
(3)拓展迁移:如图3,在△ABC中,AB=AC,∠BAC=70°,点P在线段AB的延长线上,点D在线段CB的延长线上,在△PDE中,PD=PE,∠DPE=70°,设BP=a,请直接写出线段BD、BE之间的数量关系(用含a的式子表示)
参考答案:
【答案】(1)5;(2)4;(3)BD﹣BE =2acos55°.
【解析】试题分析:(1)先判断出∠BPE=∠CAD,进而判断出△PBE≌△ACD,即可得出BD+BE=BC=5;
(2)先构造出等边三角形,再判断出∠BPE=∠FPD,进而判断出△PBE≌△PFD,即可得出BD+BE=BF=4;
(3)类似于(2)的方法判断出△PBE≌△PFD得出BE=DF,再判断出BF=2BG,利用用锐角三角函数求出BG=acos55°,即可BD-BE=BF=2acos55°.
试题解析:解:(1)∵△ABC和△PDE是等边三角形,
∴PE=PD,AB=AC,∠DPE=∠CAB=60°,
∴∠BPE=∠CAD,
∴△PBE≌△ACD,
∴BE=CD,
∴BD+BE=BD+CD=BC=5,
故答案为5;
(2)如图2,过点P作PF∥AC交BC于F,
∴△FPB是等边三角形,
∴BF=PF=PB=AB﹣AP=4,∠BPF=60°,
∵△PDE是等边三角形,
∴PD=PE,∠DPE=60°,
∴∠BPE=∠FPD,
∴△PBE≌△PFD,
∴BE=DF,
∴BD+BE=BD+DF=BF=4;
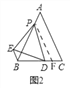
(3)如图3,
过点P作PF∥AC交BC于F,
∴∠BPF=∠BAC=70°,∠PFB=∠C,
∵AB=AC,∠BAC=70°,
∴∠ABC=∠C=55°,
∴∠PFB=∠C=∠PBF=55°,
∴PF=PB=a,
∵∠BPF=∠DPE=70°,
∴∠DPF=∠EPB,
∵PD=PE,
∴△PBE≌△PFD,
∴BE=DF,
过点P作PG⊥BC于G,
∴BF=2BG,
在Rt△BPG中,∠PBD=55°,
∴BG=BPcos∠PBD=acos55°,
∴BF=2BG=2acos55°,
∴BD﹣BE=BD﹣DF=BF=2acos55°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
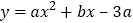 经过
经过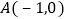 、
、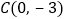 两点,与x轴交于另一点B.
两点,与x轴交于另一点B. 求此抛物线的解析式;
求此抛物线的解析式; 已知点
已知点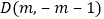 在第四象限的抛物线上,求点D关于直线BC对称的点
在第四象限的抛物线上,求点D关于直线BC对称的点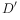 的坐标.
的坐标.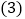 在
在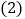 的条件下,连接BD,问在x轴上是否存在点P,使
的条件下,连接BD,问在x轴上是否存在点P,使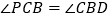 ?若存在,请求出P点的坐标;若不存在,请说明理由.
?若存在,请求出P点的坐标;若不存在,请说明理由.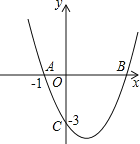
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分剪下,拼成右边的矩形,由图形①到图形②的变化过程能够验证的一个等式是( )
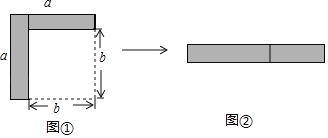
A. a(a+b)=a2+ab B. a2﹣b2=(a+b)(a﹣b)
C. (a+b)2=a2+2ab+b2 D. a(a﹣b)=a2﹣ab
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上顺次有
 、
、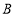 、
、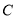 三点,分别表示数
三点,分别表示数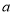 、
、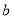 、
、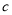 ,并且满足
,并且满足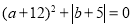 ,
,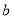 与
与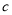 互为相反数.一只电子小蜗牛从
互为相反数.一只电子小蜗牛从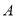 点向正方向移动,速度为2个单位/秒.
点向正方向移动,速度为2个单位/秒.(1)请求出
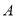 、
、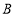 、
、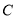 三点分别表示的数.
三点分别表示的数.(2)运动多少秒时,小蜗牛到点
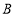 的距离为1个单位长度.
的距离为1个单位长度.(3)设点
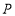 在数轴上点A的右边,且点
在数轴上点A的右边,且点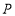 分别到点
分别到点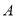 、点
、点 、点
、点 的距离之和是20,那么点
的距离之和是20,那么点 所表示的数是_____.
所表示的数是_____. -
科目: 来源: 题型:
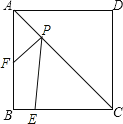
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB的中点,P为AC上一个动点,则PF+PE的最小值为( )
A. 2
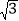 B. 4 C.
B. 4 C. 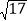 D. 2
D. 2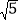
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P为抛物线y=x2+2x﹣3在第一象限内的一个动点,且P关于原点的对称点P′恰好也落在该抛物线上,则点P′的坐标为( )
A. (﹣1,﹣1) B. (﹣2,﹣
 ) C. (﹣
) C. (﹣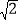 ,﹣2
,﹣2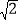 ﹣1) D. (﹣
﹣1) D. (﹣ ,﹣2
,﹣2 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方
形,然后按图②的方式拼成一个正方形。
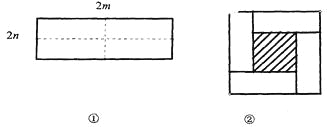
(1)你认为图②中的阴影部分的正方形的边长等于_________________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积。
方法①_________________________________________________________.
方法②_________________________________________________________.
(3)观察图②,你能写出
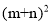 ,
, ,mn这三个代数式间的等量关系吗?
,mn这三个代数式间的等量关系吗?
相关试题

