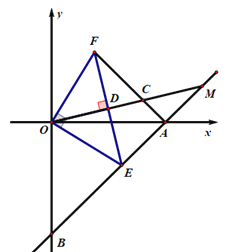
【题目】如图,直线AB与x轴交于点A(4,0),与y轴交于点B(0,-4),若点E在线段AB上,OE⊥OF,且OE=OF,连接AF.
(1)猜想线段AF与BE之间的关系,并证明;
(2)过点O作OM⊥EF垂足为D,OM分别交AF、BA的延长线于点C、M若BE=![]() ,求CF的长.
,求CF的长.
参考答案:
【答案】(1) AF=BE,证明见解析 (2)CF=![]()
【解析】
(1)由已知可得:∠FOE=∠AOB=90°,减去公共角∠AOE可得:∠FOA=∠EOB,又因为OE=OF,OA=OB,可证FOAEOB,即可得AF与BE相等.
(2)由(1)可得∠FAO=∠OBA=∠OAB=45°,可得∠FAE=90°,由A,B坐标可求得AB=4![]() ,又AF=BE=
,又AF=BE=![]() ,得AE的长.连接EC,根据等腰三角形的“三线合一”可得OM垂直平分EF,则FC=EC,设FC=EC=x,则AC=
,得AE的长.连接EC,根据等腰三角形的“三线合一”可得OM垂直平分EF,则FC=EC,设FC=EC=x,则AC=![]() ,在直角三角形AEC中,根据勾股定理列出方程,代入数值即可求得CF的长.
,在直角三角形AEC中,根据勾股定理列出方程,代入数值即可求得CF的长.
(1) AF=BE,证明:
∵直线AB与x轴交于点A(4,0),与y轴交于点B(0,-4)
∴OA=OB=4
∵OE⊥OF
∴∠FOE=∠AOB=90°
∴∠FOE-∠AOE=∠AOB-∠AOE
即∠FOA=∠EOB
在FOA和EOB中
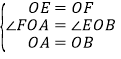
∴FOAEOB(SAS)
∴AF=BE
(2)连接EC.
∵OA=OB=4,∠AOB=90°
∴∠OBA=∠OAB=45°,AB=![]() 4
4![]()
由(1)得:FOAEOB
∴∠FAO=∠OBA=∠OAB=45°,AF=BE=![]()
∴∠FAE=90°,AE=![]()
∵OE=OF, OM⊥EF
∴OM垂直平分EF
∴FC=EC
设FC=EC=x,则AC=![]()
根据勾股定理得:
![]()
解得![]()
∴CF=![]()
-
科目: 来源: 题型:
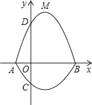
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣
 ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在解方程
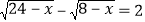 时运用了下面的方法:由
时运用了下面的方法:由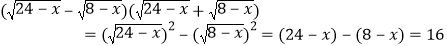 ,又由
,又由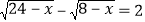 可得
可得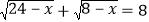 ,将这两式相加可得
,将这两式相加可得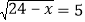 ,将
,将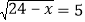 两边平方可解得
两边平方可解得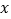 =-1,经检验
=-1,经检验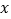 =-1是原方程的解.
=-1是原方程的解.请你参考小明的方法,解下列方程:
(1)
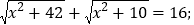
(2)
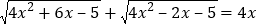 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BE∥CF,且BE=CF,若BE、CF分别平分∠ABC和∠BCD.
(1)请判断AB与CD是否平行?并说明你的理由.
(2)CE、BF相等吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为8,动点M从点B出发,沿B→A→C→B的方向以每秒3个单位长度的速度运动,动点N从点C出发,沿C→A→B-C的方向以每秒2个单位长度的速度运动.
(1)若动点M、N同时出发,经过几秒第一次相遇?
(2)若动点M、N同时出发,且其中一点到达终点时,另一点即停止运动.在△ABC的边上是否存在一点D,使得以点A、M、N、D为顶点的四边形为平行四边形?若存在,求此时运动的时间
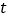 及点D的具体位置;若不存在,请说明理由.
及点D的具体位置;若不存在,请说明理由.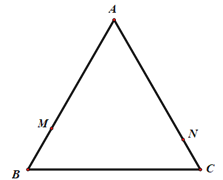
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
相关试题

