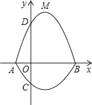
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.
参考答案:
【答案】(1) A(﹣1,0),B(3,0);(2)存在,P(![]() );(3) m=﹣1或﹣
);(3) m=﹣1或﹣![]() .
.
【解析】试题分析:(1)将![]() 化为交点式,即可得到
化为交点式,即可得到![]() 两点的坐标;
两点的坐标;
(2)先用待定系数法得到抛物线C1的解析式,过点P作PQ∥y轴,交BC于Q,用待定系数法得到直线BC的解析式,再根据三角形的面积公式和配方法得到![]() 面积的最大值;
面积的最大值;
(3)先表示出![]() 再分两种情况:①
再分两种情况:①![]() 时;
时;
②![]() 时,讨论即可求得
时,讨论即可求得![]() 的值.
的值.
试题解析:(1)![]()
∵m≠0,
∴当y=0时,![]()
∴A(1,0),B(3,0);
(2)设![]() ,将A. B.C三点的坐标代入得:
,将A. B.C三点的坐标代入得:
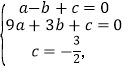 解得
解得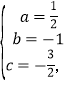
故![]()
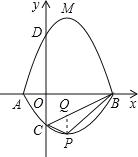
如图:过点P作PQ∥y轴,交BC于Q,
由B.C的坐标可得直线BC的解析式为:![]()
设![]() 则
则![]()
![]()
![]()
当![]() 时,
时,![]() 有最大值
有最大值![]()
![]()
![]()
(3)![]()
顶点M坐标(1,4m),
当x=0时,y=3m,
∴D(0,3m),B(3,0),
![]()
![]()
![]()
当△BDM为Rt△时有:![]() 或
或![]()
![]() 时有:
时有:![]()
解得m=1(∵m<0,∴m=1舍去);
![]() 时有:
时有:![]()
解得![]() (
(![]() 舍去).
舍去).
综上,m=1或![]() 时,
时,![]() 为直角三角形.
为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,给出下列的条件,能判断它是平行四边形的是( )
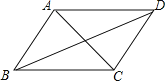
A. AB//CD, AD=BCB. ∠B=∠C,∠A=∠D
C. AB=AD, BC=CDD. AB=CD, AD=BC
-
科目: 来源: 题型:
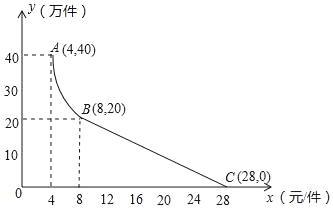
查看答案和解析>>【题目】月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种电子产品的年利润s(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值.
(3)假设公司的这种电子产品第一年恰好按年利润s(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格x(元)定在8元以上(x>8),当第二年的年利润不低于103万元时,请结合年利润s(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
-
科目: 来源: 题型:
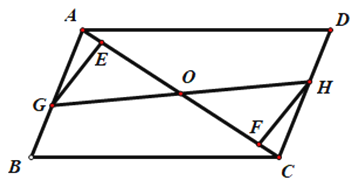
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
(1)求证:EG//FH;
(2)GH、EF互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在解方程
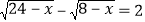 时运用了下面的方法:由
时运用了下面的方法:由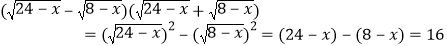 ,又由
,又由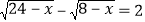 可得
可得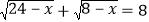 ,将这两式相加可得
,将这两式相加可得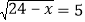 ,将
,将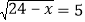 两边平方可解得
两边平方可解得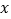 =-1,经检验
=-1,经检验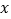 =-1是原方程的解.
=-1是原方程的解.请你参考小明的方法,解下列方程:
(1)
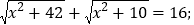
(2)
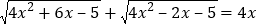 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BE∥CF,且BE=CF,若BE、CF分别平分∠ABC和∠BCD.
(1)请判断AB与CD是否平行?并说明你的理由.
(2)CE、BF相等吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与x轴交于点A(4,0),与y轴交于点B(0,-4),若点E在线段AB上,OE⊥OF,且OE=OF,连接AF.
(1)猜想线段AF与BE之间的关系,并证明;
(2)过点O作OM⊥EF垂足为D,OM分别交AF、BA的延长线于点C、M若BE=
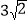 ,求CF的长.
,求CF的长.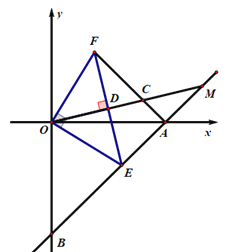
相关试题

