【题目】如图,抛物线y= ![]() x2﹣
x2﹣ ![]() x+c与y轴交于点A(0,﹣
x+c与y轴交于点A(0,﹣ ![]() ),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.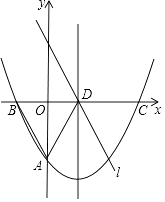
(1)求AB所在直线的函数表达式;
(2)请你判断△ABD的形状并证明你的结论;
(3)点E在线段AD上运动且与点A、D不重合,点F在直线l上运动,且∠BEF=60°,连接BF,求出△BEF面积的最小值.
解:
参考答案:
【答案】
(1)
解:将A(0,﹣ ![]() )代入抛物线解析式,得c=﹣
)代入抛物线解析式,得c=﹣ ![]() ,
,
∴y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ,
,
当y=0时, ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() =0化简,得
=0化简,得
x2﹣2x﹣3=0,
∵(x+1)(x﹣3)=0,
∴x1=﹣1,x2=3,
点B(﹣1,0),点C(3,0),
设直线AB的解析式为y=kx+b,将A、B点坐标代入函数解析式,得
![]() ,解得
,解得 ![]() ,
,
直线AB的解析式为y=﹣ ![]() x﹣
x﹣ ![]()
(2)
解:△ABD是等边三角形,
∵点B(﹣1,0),点D(1,0),
∴OB=OD=1,
在△BOA和△DOA中, 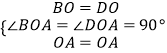 ,
,
∴△BOA≌△DOA,
∴BA=DA.
tan∠ABO= ![]() =
= ![]() =
= ![]() ,
,
∴∠ABO=60°,
∴△ABD是等边三角形
(3)
如图
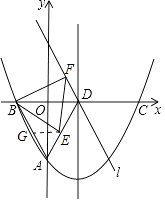 ,
,
过点E作EG∥x轴,交AB于点G,
∵△ABD是等边三角形,
∴∠BAD=∠ABD=∠ADB=60°,
∴∠AEG=∠AGE=60°,
∴△AEG是等边三角形,
∴AE=AG,∴DE=BG.
∵AB∥l,
∴∠EDF=∠BGE=120°,
∴∠GBE+∠GEB=60°,∠DEF+∠GEB=60°,
∴∠GBE=∠DEF,
在△BEG和△EFD中 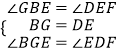 ,
,
∴△BEG≌△EFD,
∴BE=EF,
∵∠BEF=60°,
∴△BEF是等边三角形,
∴S△BEF= ![]() BE2,当BE⊥AD时,BE的长度最小,△BEF的面积最小,
BE2,当BE⊥AD时,BE的长度最小,△BEF的面积最小,
此时BE=ABsin60°= ![]() ,
,
S△BEF最小= ![]() BE2=
BE2= ![]()
【解析】(1)根据待定系数法,可得函数解析式,根据自变量与函数值的对应关系,可得点的坐标,根据待定系数法,可得函数解析式;(2)根据全等三角形的判定与性质,可得BA与DA,根据正切函数的定义,可得∠ABO,根据等边三角形的判定,可得答案;(3)根据平行线的性质,可得∠AEG=∠AGE=60°,根据全等三角形的判定与性质,可得BE=EF,根据等边三角形的判定,可得△BEF是等边三角形,根据等边三角形的面积,根据垂线段最短,可得BE的长,可得答案.
-
科目: 来源: 题型:
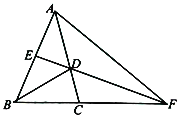
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD是∠B的平分线,交AC于点D,E是AB中点,ED交BC的延长线于点F.求证:AB=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为奖励在演讲比赛中获奖的同学,班主任派学习委员小明为获奖同学买奖品,要求每人一件,小明到文具店看了商品后,决定奖品在钢笔和笔记本中选择,若买4个笔记本和2支钢笔,则需86元;若买3个笔记本和1支钢笔,则需57元.
(1)求购买一个笔记本、一支钢笔分别为多少元;
(2)售货员提示,买钢笔有优惠,具体方法是:如果买钢笔超过10支,那么超出部分可以享受8折优惠.买15支钢笔,20个笔记本,一共需要花多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△DEF的各顶点分别在双曲线y=
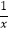 ,y=
,y= 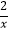 ,y=
,y= 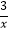 在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC﹣S△DEF=( )
在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC﹣S△DEF=( ) 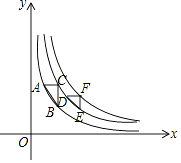
A.
B.
C.
D.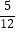
-
科目: 来源: 题型:
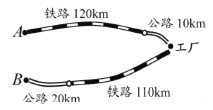
查看答案和解析>>【题目】如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5元/(吨千米),铁路运价为1.2元/(吨千米),这两次运输共支出公路运费15 000元,铁路运费97 200元,请计算这批产品的销售款比原料费和运输费的和多多少元?
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
甲:
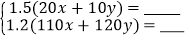
乙
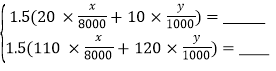 :
:根据甲,乙两名同学所列方程组,请你分别指出未知数x,y表示的意义,然后在等式右边补全甲、乙两名同学所列方程组.
甲:x表示 ,y表示 ;
乙:x表示 ,y表示 .
(2)甲同学根据他所列方程组解得x=300,请你帮他解出y的值,并解决该实际问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,射线AM平分∠BAC,AB=8,cos∠ACB=
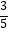 ,点P为射线AM上一点,且PB=PC,则四边形ABPC的面积为 .
,点P为射线AM上一点,且PB=PC,则四边形ABPC的面积为 . 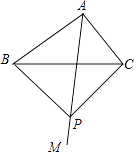
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;并用含α的式子表示∠AMB的度数;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.

相关试题

