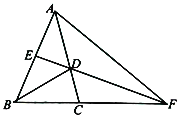
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD是∠B的平分线,交AC于点D,E是AB中点,ED交BC的延长线于点F.求证:AB=CF.
参考答案:
【答案】见解析
【解析】
根据等腰三角形的性质,可得∠ABC=∠ACB=72°,根据角平分线的性质,可得∠1=∠2=36°,可得DA与DB的关系,根据线段垂直平分线的判定与性质,可得FA与FB的关系,可得∠FAB与∠ABC的关系,根据三角形外角的关系,可得∠AFC=∠ACB-∠3=36°,根据等腰三角形的判定,可得AC与CF的关系,根据等量代换,可得答案.
证明:如图,连接AF,
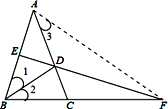
∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=72°.
∵BD平分∠ABC,
∴∠1=∠2=36°,
∴∠1=∠BAD=36°,
∴DA=DB.
∵AE=BE,
∴FE⊥AB,即FE是AB的垂直平分线,
∴FA=FB,
∴∠FAB=∠ABC=72°,
∴∠3=∠FAB-∠BAC=36°,
∵∠ACB=∠3+∠AFC,
∴∠AFC=∠ACB-∠3=36°,
∴∠3=∠AFC,
∴AC=CF,
∴AB=CF.
-
科目: 来源: 题型:
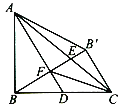
查看答案和解析>>【题目】如图,点 D 是等腰直角 △ABC 腰 BC 上的中点,点B 、B′ 关于 AD 对称,且 BB′ 交AD 于 F,交 AC 于 E,连接 FC 、 AB′,下列说法:① ∠BAD=30°; ② ∠BFC=135°;③ AF=2B′ C;正确的个数是()
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠A=140°,∠D=80°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小华通过学习函数发现:若二次函数y=ax2+bx+c(a≠0)的图象经过点(x1 , y1),(x2 , y2)(x1<x2),若y1y2<0,则方程ax2+bx+c=0(a≠0)的一个根x0的取值范围是x1<x0<x2 , 请你类比此方法,推断方程x3+x﹣1=0的实数根x0所在范围为( )
A.﹣ <x0<0
<x0<0
B.0<x0<
C. <x0<1
<x0<1
D.1<x0<
-
科目: 来源: 题型:
查看答案和解析>>【题目】为奖励在演讲比赛中获奖的同学,班主任派学习委员小明为获奖同学买奖品,要求每人一件,小明到文具店看了商品后,决定奖品在钢笔和笔记本中选择,若买4个笔记本和2支钢笔,则需86元;若买3个笔记本和1支钢笔,则需57元.
(1)求购买一个笔记本、一支钢笔分别为多少元;
(2)售货员提示,买钢笔有优惠,具体方法是:如果买钢笔超过10支,那么超出部分可以享受8折优惠.买15支钢笔,20个笔记本,一共需要花多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△DEF的各顶点分别在双曲线y=
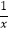 ,y=
,y= 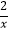 ,y=
,y= 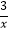 在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC﹣S△DEF=( )
在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC﹣S△DEF=( ) 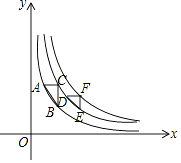
A.
B.
C.
D.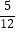
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
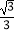 x2﹣
x2﹣  x+c与y轴交于点A(0,﹣
x+c与y轴交于点A(0,﹣  ),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.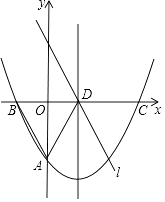
(1)求AB所在直线的函数表达式;
(2)请你判断△ABD的形状并证明你的结论;
(3)点E在线段AD上运动且与点A、D不重合,点F在直线l上运动,且∠BEF=60°,连接BF,求出△BEF面积的最小值.
解:
相关试题

