【题目】如图,在△ABC中,∠BAC=90°,射线AM平分∠BAC,AB=8,cos∠ACB= ![]() ,点P为射线AM上一点,且PB=PC,则四边形ABPC的面积为 .
,点P为射线AM上一点,且PB=PC,则四边形ABPC的面积为 . 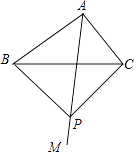
参考答案:
【答案】49
【解析】解:∵在△ABC中,∠BAC=90°,AB=8,cos∠ACB= ![]() , ∴设AC=3k,BC=5k,
, ∴设AC=3k,BC=5k,
∴AB=4k,
∴k=2,
∴BC=10,AC=6,
过P作PE⊥AB于E,PF⊥于F,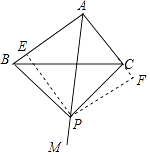
∴四边形AEPF是矩形,
∵射线AM平分∠BAC,
∴PE=PF,
∴矩形AEPF是正方形,
在Rt△PBE与Rt△PFC中 ![]() ,
,
∴Rt△PBE≌Rt△PFC,
∴BE=CF,
∴AE=AF=7,
∴四边形ABPC的面积=正方形AEPF的面积=7×7=49,
所以答案是:49.
【考点精析】认真审题,首先需要了解角平分线的性质定理(定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△DEF的各顶点分别在双曲线y=
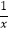 ,y=
,y= 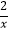 ,y=
,y= 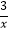 在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC﹣S△DEF=( )
在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC﹣S△DEF=( ) 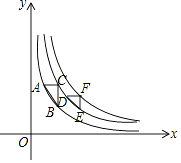
A.
B.
C.
D.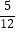
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
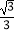 x2﹣
x2﹣  x+c与y轴交于点A(0,﹣
x+c与y轴交于点A(0,﹣  ),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.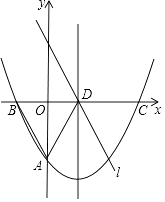
(1)求AB所在直线的函数表达式;
(2)请你判断△ABD的形状并证明你的结论;
(3)点E在线段AD上运动且与点A、D不重合,点F在直线l上运动,且∠BEF=60°,连接BF,求出△BEF面积的最小值.
解: -
科目: 来源: 题型:
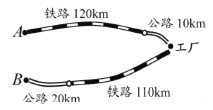
查看答案和解析>>【题目】如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5元/(吨千米),铁路运价为1.2元/(吨千米),这两次运输共支出公路运费15 000元,铁路运费97 200元,请计算这批产品的销售款比原料费和运输费的和多多少元?
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
甲:
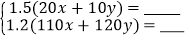
乙
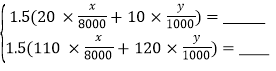 :
:根据甲,乙两名同学所列方程组,请你分别指出未知数x,y表示的意义,然后在等式右边补全甲、乙两名同学所列方程组.
甲:x表示 ,y表示 ;
乙:x表示 ,y表示 .
(2)甲同学根据他所列方程组解得x=300,请你帮他解出y的值,并解决该实际问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;并用含α的式子表示∠AMB的度数;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】南水北调中线工程北京段干线工程起自房山北拒马河,经房山区至大宁水库,穿永定河,过丰台,沿西四环路北上至终点颐和园团城湖,全长80公里. 主要采取地下涵管压力输水方式,在输水过程中全程计量、跟踪监测、精细调度、高效配置,确保最大限度利用南水. 北京严格遵循南水北调工程“三先三后”原则,科学制定用水计划,研究确立了“节、喝、存、补”的用水方针,2017-2018年度入京水量达12.10亿立方米,成为历年来北京调水最多的一个调水年度. 如图,在铺设地下管道的时候,需要把拒马河沿线的管道l中的水引到房山水站A,B两处.

工人师傅设计了一种最节省材料的修建方案如下:


请回答:工人师傅的画图依据是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD的四个顶点A、B、C、D的坐标分别为(﹣1,1)、(﹣1,﹣3)、(5,3)、(1,3),则其对称轴的函数表达式为 .

相关试题

