【题目】已知二次函数y=ax2+bx+c的图象C经过(﹣5,0),(0, ![]() ),(1,6)三点,直线l的解析式为y=2x﹣3.
),(1,6)三点,直线l的解析式为y=2x﹣3.
(1)求抛物线C的解析式;
(2)判断抛物线C与直线l有无交点;
(3)若与直线l平行的直线y=2x+m与抛物线C只有一个公共点P,求点P的坐标.
参考答案:
【答案】
(1)解:∵二次函数y=ax2+bx+c的图象抛物线C经过(﹣5,0),(0, ![]() ),(1,6)三点,
),(1,6)三点,
∴ 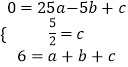 ,解得
,解得 ![]() ,
,
∴抛物线C的函数解析式为:y= ![]() x2+3x+
x2+3x+ ![]()
(2)解:∵由(1)得抛物线C的函数解析式为:y= ![]() x2+3x+
x2+3x+ ![]() ,
,
∴代入y=2x﹣3得2x﹣3=x2+3x+ ![]() ,
,
整理得 ![]() x2+x+
x2+x+ ![]() =0,
=0,
∵△=12﹣4× ![]() ×
× ![]() =﹣10<0,
=﹣10<0,
∴方程无实数根,即抛物线C与直线l无公共点
(3)解:∵与l平行的直线y=2x+m与抛物线G只有一个公共点P,
∴ 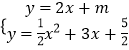 ,消去y得,
,消去y得, ![]() x2+x+
x2+x+ ![]() ﹣m=0①,
﹣m=0①,
∵抛物线C与直线y=2x+m只有一个公共点P,
∴△=12﹣4× ![]() ×(
×( ![]() ﹣m)=0,解得m=2,
﹣m)=0,解得m=2,
把m=2代入方程①得, ![]() x2+x+
x2+x+ ![]() ﹣2=0,解得x=﹣1,
﹣2=0,解得x=﹣1,
把x=﹣1代入直线y=2x+2得,y=0,
∴P(﹣1,0).
【解析】(1)直接把点(﹣5,0),(0, ![]() ),(1,6)代入二次函数y=ax2+bx+c,求出a、b、c的值即可;(2)把(1)中求出的抛物线的解析式与直线l的解析式y=2x﹣3组成方程组,再根据一元二次方程根的判别式即可得出结论;(3)把直线y=2x+m与抛物线C的解析式组成方程组,根据只有一个公共点P可知△=0,求出m的值,故可得出P点坐标即可.
),(1,6)代入二次函数y=ax2+bx+c,求出a、b、c的值即可;(2)把(1)中求出的抛物线的解析式与直线l的解析式y=2x﹣3组成方程组,再根据一元二次方程根的判别式即可得出结论;(3)把直线y=2x+m与抛物线C的解析式组成方程组,根据只有一个公共点P可知△=0,求出m的值,故可得出P点坐标即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D、E分别是AB、AC上的点,BE交CD于点O,BO=CO,DO=EO,AB=AC,AD=AE则图中有___________对全等三角形( )

A. 2对 B. 3对 C. 4对 D. 5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,D、E、 F分别是△ABC的三边的延长线上一点,且AB=BF,BC=CD,AC=AE,
 =5cm2,则
=5cm2,则 的值是( )
的值是( )
A. 15 cm2 B. 20 cm2 C. 30 cm2 D. 35 cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与x交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3)

(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,AC上的中线BD把三角形的周长分为15㎝和30㎝的两个部分,求:三角形的三边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数y=
 x2+
x2+  的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数y= x2+
x2+  的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y= x2+
x2+  的自变量x的取值范围是
的自变量x的取值范围是
(2)下表是y与x的几组对应值.x
…
﹣3
﹣2
﹣1
﹣

﹣



1
2
3
…
y
…


﹣

﹣

﹣





m
…
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1, ),结合函数的图象,写出该函数的其它性质(一条即可) .
),结合函数的图象,写出该函数的其它性质(一条即可) . -
科目: 来源: 题型:
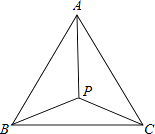
查看答案和解析>>【题目】已知:如图,P为等边△ABC内一点,∠APB=113°,∠APC=123°,试说明:以AP,BP,CP为边长可以构成一个三角形,并确定所构成三角形的各内角的度数.
相关试题

