【题目】在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于点O,线段OA,OB的中点分别为E,F.
(1)求证:△FOE≌△DOC;
(2)求sin∠OEF的值;
(3)若直线EF与线段AD,BC分别相交于点G,H,求 ![]() 的值.
的值.
参考答案:
【答案】
(1)
证明:∵EF是△OAB的中位线,
∴EF∥AB,EF= ![]() AB,
AB,
而CD∥AB,CD= ![]() AB,
AB,
∴EF=CD,∠OEF=∠OCD,∠OFE=∠ODC,
∴△FOE≌△DOC

(2)
解:∵EF∥AB,
∴∠OEF=∠CAB,
∵在Rt△ABC中,AC= ![]() =
= ![]() =
= ![]() BC,
BC,
∴sin∠OEF=sin∠CAB= ![]() =
= ![]() =
= ![]()
(3)
解:∵AE=OE=OC,EF∥CD,
∴△AEG∽△ACD,
∴ ![]() =
= ![]() ,即EG=
,即EG= ![]() CD,
CD,
同理FH= ![]() CD,
CD,
∴ ![]() =
= ![]() =
= ![]()
【解析】(1)由EF是△OAB的中位线,利用中位线定理,得EF∥AB,EF= ![]() AB,又CD∥AB,CD=
AB,又CD∥AB,CD= ![]() AB,可得EF=CD,由平行线的性质可证△FOE≌△DOC;(2)由平行线的性质可知∠OEF=∠CAB,利用sin∠OEF=sin∠CAB=
AB,可得EF=CD,由平行线的性质可证△FOE≌△DOC;(2)由平行线的性质可知∠OEF=∠CAB,利用sin∠OEF=sin∠CAB= ![]() ,由勾股定理得出AC与BC的关系,再求正弦值;(3)由(1)可知AE=OE=OC,EF∥CD,则△AEG∽△ACD,利用相似比可得EG=
,由勾股定理得出AC与BC的关系,再求正弦值;(3)由(1)可知AE=OE=OC,EF∥CD,则△AEG∽△ACD,利用相似比可得EG= ![]() CD,同理得FH=
CD,同理得FH= ![]() CD,又AB=2CD,代入
CD,又AB=2CD,代入 ![]() 中求值.
中求值.
【考点精析】本题主要考查了勾股定理的概念和三角形中位线定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=
 ,AC=
,AC= 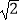 ,BC=1.
,BC=1.
(1)求证:∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】中国国际动漫节以“动漫的盛会,人民的节日”为宗旨,以“动漫我的城市,动漫我的生活”为主题,已在杭州成功举办七届.目前,它成为国内规模最大、交易最旺、影响最广的动漫专业盛会. 下面是自首届以来各届动漫产品成交金额统计图表(部分未完成):

(1)请根据所给的信息将统计图表补充完整;
(2)从哪届开始成交金额超过百亿元?相邻两届中,哪两届的成交金额增长最快?
(3)求第五届到第七届的平均增长率,并用它预测第八届中国国际动漫节的成交金额(精确到亿元) -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面上,七个边长为1的等边三角形,分别用①至⑦表示(如图).从④⑤⑥⑦组成的图形中,取出一个三角形,使剩下的图形经过一次平移,与①②③组成的图形拼成一个正六边形

(1)你取出的是哪个三角形?写出平移的方向和平移的距离;
(2)将取出的三角形任意放置在拼成的正六边形所在平面,问:正六边形没有被三角形盖住的面积能否等于 ?请说明理由.
?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数y=kx2+(2k+1)x+1(k为实数)
(1)写出其中的两个特殊函数,使它们的图象不全是抛物线,并在同一直角坐标系中,用描点法画出这两个特殊函数的图象;
(2)根据所画图象,猜想出:对任意实数k,函数的图象都具有的特征,并给予证明;
(3)对任意负实数k,当x<m时,y随着x的增大而增大,试求出m的一个值. -
科目: 来源: 题型:
查看答案和解析>>【题目】图形既关于点O中心对称,又关于直线AC,BD对称,AC=10,BD=6,已知点E,M是线段AB上的动点(不与端点重合),点O到EF,MN的距离分别为h1 , h2 , △OEF与△OGH组成的图形称为蝶形.

(1)求蝶形面积S的最大值;
(2)当以EH为直径的圆与以MQ为直径的圆重合时,求h1与h2满足的关系式,并求h1的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运40千克,A型机器人搬运1200千克所用时间与B型机器人搬运800千克所用时间相等.设B型机器人每小时搬运化工原料x千克,根据题意可列方程为( )
A. =
= 
B. =
= 
C. =
= 
D. =
= 
相关试题

