搜索
【题目】A，B两种机器人都被用来搬运化工原料，A型机器人比B型机器人每小时多搬运40千克，A型机器人搬运1200千克所用时间与B型机器人搬运800千克所用时间相等．设B型机器人每小时搬运化工原料x千克，根据题意可列方程为（ ）
A.
= 
B.
=
C.
= 
D. = 
参考答案：
【答案】A
【解析】解：设B型机器人每小时搬运化工原料x千克，则A型机器人每小时搬运化工原料（x+40）千克，
∵A型机器人搬运1200千克所用时间与B型机器人搬运800千克所用时间相等，
∴ 
= 
．
故选A．
根据A、B两种机器人每小时搬运化工原料间的关系可得出A型机器人每小时搬运化工原料（x+40）千克，再根据A型机器人搬运1200千克所用时间与B型机器人搬运800千克所用时间相等即可列出关于x的分式方程，由此即可得出结论．本题考查了由实际问题抽象出分式方程，解题的关键是根据数量关系列出关于x的分式方程．本题属于基础题，难度不大，解决该题型题目时，根据数量关系列出方程是关键．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2BC=2CD，对角线AC与BD相交于点O，线段OA，OB的中点分别为E，F．
（1）求证：△FOE≌△DOC；
（2）求sin∠OEF的值；
（3）若直线EF与线段AD，BC分别相交于点G，H，求
的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】设函数y=kx2+（2k+1）x+1（k为实数）
（1）写出其中的两个特殊函数，使它们的图象不全是抛物线，并在同一直角坐标系中，用描点法画出这两个特殊函数的图象；
（2）根据所画图象，猜想出：对任意实数k，函数的图象都具有的特征，并给予证明；
（3）对任意负实数k，当x＜m时，y随着x的增大而增大，试求出m的一个值． -
科目： 来源： 题型：
查看答案和解析>>【题目】图形既关于点O中心对称，又关于直线AC，BD对称，AC=10，BD=6，已知点E，M是线段AB上的动点（不与端点重合），点O到EF，MN的距离分别为h1 ， h2 ， △OEF与△OGH组成的图形称为蝶形．
（1）求蝶形面积S的最大值；
（2）当以EH为直径的圆与以MQ为直径的圆重合时，求h1与h2满足的关系式，并求h1的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】下面图形都是由同样大小的平行四边形按一定的规律组成，其中，第①个图形一共有1个平行四边形，第②个图形一共有5个平行四边形，第③个图形一共有11个平行四边形，……，则第⑥个图形中平行四边形的个数为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某兴趣小组借助无人飞机航拍校园．如图，无人飞机从A处水平飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°，B处的仰角为30°．已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度．（结果保留根号）
-
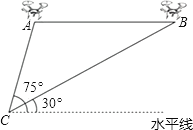
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在扇形AOB中∠AOB=90°，正方形CDEF的顶点C是
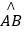的中点，点D在OB上，点E在OB的延长线上，当正方形CDEF的边长为2 
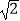时，则阴影部分的面积为（ ）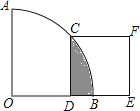 
A.2π﹣4
B.4π﹣8
C.2π﹣8
D.4π﹣4
相关试题
