Question

【题目】如图，Rt△ABC中，∠C=90°，AB=5，AC=3，D点从BC的中点到C点运动，点E在AD上，以E为圆心的⊙E分别与AB、BC相切，则⊙E的半径R的取值范围为（　　）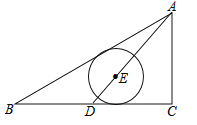

A.≤R≤
B.≤R≤
C.≤R≤2
D.1≤R≤

Answer 1

【答案】B
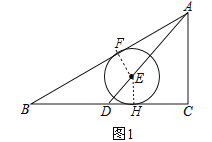
【解析】解：当点E在AD上，AD为△ABC的中线，如图1，作EH⊥BC于H，EF⊥AB于F，
∵以E为圆心的⊙E分别与AB、BC相切，
∴EH=EF=R，
在Rt△ABC中，∵∠C=90°，AB=5，AC=3，
∴BC==4，
∵点D为BC的中点，
∴BD=CD=2，
在Rt△ADC中，AD== ，
∵EH∥AC，
∴△DEH∽△DAC，
∴== ， 即== ，
∴DE=R，DH=R，
∴AE=AD﹣DE=﹣R，BH=BD+DH=2+R，
∵以E为圆心的⊙E分别与AB、BC相切，
∴BF=BH=2+R
∴AF=AB﹣BF=3﹣R，
在Rt△AEF中，∵EF2+AF2=AE2 ，
∴R2+（3﹣R）2=（﹣R）2 ， 解得R=；
当点D运动到点C的位置，如图2，作EF⊥AB于F，
∵以E为圆心的⊙E分别与AB、BC相切，
∴EC=EF=R，
∴AE=AC﹣EC=3﹣R，
∵∠FAE=∠CAB，
∴Rt△AFE∽Rt△ACB，
∴= ， 即= ， 解得R= ，
∴当D点从BC的中点到C点运动，点E在AD上，以E为圆心的⊙E分别与AB、BC相切，则⊙E的半径R的取值范围为≤R≤ ．
故选B．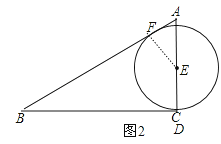


【考点精析】掌握切线的性质定理是解答本题的根本，需要知道切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．