【题目】如图,在△ABC中,∠A=90°,AB=AC=2,点O是边BC的中点,半圆O与△ABC相切于点D、E,则阴影部分的面积等于( )
A.1﹣![]()
B.![]()
C.1﹣![]()
D.![]()
参考答案:
【答案】B
【解析】解:连接OD,OE,
∵半圆O与△ABC相切于点D、E,
∴OD⊥AB,OE⊥AC,
∵在△ABC中,∠A=90°,AB=AC=2,
∴四边形ADOE是正方形,△OBD和△OCE是等腰直角三角形,
∴OD=OE=AD=BD=AE=EC=1,
∴∠ABC=∠EOC=45°,
∴AB∥OE,
∴∠DBF=∠OEF,
在△BDF和△EOF中,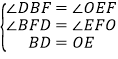 ,
,
∴△BDF≌△EOF(AAS),
∴S阴影=S扇形DOE=![]() ×π×12=
×π×12=![]() .
.
故选B.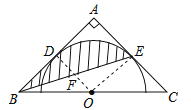
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D,过D作半圆的切线与边AC交于点E,过E作EF∥AB,与BC交于点F.若AB=20,OF=7.5,则CD的长为( )

A.7
B.8
C.9
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于D,且AE平分∠BAC,求∠EAD的度数.
(2)上题中若∠B=40°,∠C=80°改为∠C>∠B,其他条件不变,请你求出∠EAD与∠B、∠C之间的数列关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点,
研究(1):如果沿直线DE折叠,则∠BDA′与∠A的关系是 .
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为( )
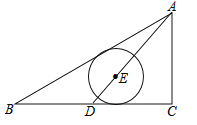
A. ≤R≤
≤R≤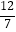
B. ≤R≤
≤R≤
C. ≤R≤2
≤R≤2
D.1≤R≤
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1.将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.如图2.若骰子的初始位置为图1所示的状态,那么按上述规则连续完成2次变换后,骰子朝上一面的点数是________;连续完成2019次变换后,骰子朝上一面的点数是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线AB上 一点O,以O为端点画射线OC,作∠AOC的角平分线OD,作∠BOC的角平分线OE;

(1)按要求完成画图;
(2)通过观察、测量你发现∠DOE= °;
(3)补全以下证明过程:
证明:∵OD平分∠AOC(已知)
∴∠DOC= ∠AOC( )
∵OE平分∠BOC(已知)
∴∠EOC= ∠BOC( )
∵∠AOC+∠BOC= °
∴∠DOE=∠DOC+∠EOC= (∠AOC+∠BOC)= °.
相关试题

