【题目】如图(1),△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点,
研究(1):如果沿直线DE折叠,则∠BDA′与∠A的关系是 .
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.

参考答案:
【答案】(1)∠BDA′=2∠A;(2)∠BDA′+∠CEA′=2∠A;(3)∠BDA′-∠CEA′=2∠A
【解析】
试题分析:翻折问题要在图形是找着相等的量.图1中DE为折痕,有∠A=∠DA′A,再利用外角的性质可得结论∠BDA′=2∠A图2中∠A与∠DA′E是相等的,再结合四边形的内角和及互补角的性质可得结论∠BDA′+∠CEA′=2∠A图3中由于折叠∠A与∠DA′E是相等的,再两次运用三角形外角的性质可得结论.
试题解析:(1)∠BDA′=2∠A;
(2)∠BDA′+∠CEA′=2∠A,
理由:在四边形ADA′E中,∠A+∠DA′E+∠ADA′+∠A′EA=360°
∴∠A+∠DA′E=360°-∠ADA′-∠A′EA
∵∠BDA′+∠ADA′=180°,∠CEA′+∠A′EA=180°
∴∠BDA′+∠CEA′=360°-∠ADA′-∠A′EA
∴∠BDA′+∠CEA′=∠A+∠DA′E
∵△A′DE是由△ADE沿直线DE折叠而得
∴∠A=∠DA′E
∴∠BDA′+∠CEA′=2∠A;
(3)∠BDA′-∠CEA′=2∠A
理由:DA′交AC于点F,
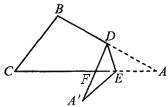
∵∠BDA′=∠A+∠DFA,∠DFA=∠A′+∠CEA′
∴∠BDA′=∠A+∠A′+∠CEA′
∴∠BDA′-∠CEA′=∠A+∠A′
∵△A′DE是由△ADE沿直线DE折叠而得
∴∠A=∠DA′E
∴∠BDA′-∠CEA′=2∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a-1的平方根是±3,3a-b+2的算术平方根是4,求a+3b的立方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,求抛物线经过A(1,0),C(0,3)两点,与x轴交于A、B两点.
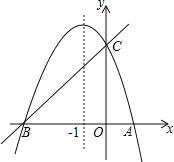
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在该抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为该抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.(提示:若平面直角坐标系内两点P(x1,y1)、Q(x2,y2),则线段PQ的长度PQ=
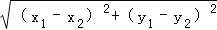 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C,
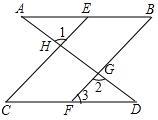
(1)说明CE∥BF.
(2)你能得出∠B=∠3和∠A=∠D这两个结论吗?若能,写出你得出结论的过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=﹣x2+x+2,则当y<0时,自变量x的取值范围是( )
A.x<﹣1或x>2 B.﹣1<x<2
C.x<﹣2或x>1 D.﹣2<x<1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2a3=a6 B.a2+a2=a4 C.3a2×2a2=6a4 D.5a﹣a=4
-
科目: 来源: 题型:
查看答案和解析>>【题目】小芳有两根长度分别为4cm和9cm的木条,他想钉一个三角形木框,桌子上有下列长度的几根木条,她应该选择的木条的长度只能是( )
A. 5cm B. 3cm C. 17cm D. 12cm
相关试题

