【题目】操作与探究 探索:在如图1至图3中,△ABC的面积为a .
(1)如图1, 延长△ABC的边BC到点D,使CD=BC,连结DA.若△ACD的面积为S1,则S1=________(用含a的代数式表示);




(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则S2= (用含a的代数式表示);
(3)在图2的基础上延长AB到点F,使BF=AB,连结FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3=__________(用含a的代数式表示).
发现:像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的_____倍.
参考答案:
【答案】(1)a;(2)2a;(3)6a;7.
【解析】(1)根据等底等高的三角形面积相等解答即可;(2)分别过A、E作BD的垂线,根据三角形中位线定理及三角形的面积公式求解即可;(3)由△BFD、△ECD及△AEF的边长为△ABC边长的一半,高与△AEF的高相等解答即可.
解:(1) ∵CD=BC, △ABC的面积为a, △ABC与△ACD的高相等,![]() ;
;
(2)分别过A、E作AG⊥BD,EF⊥BD,G、F为垂足,
则AG∥EF,∵A为CE的中点,![]() ,
,
∵BC=CD,![]() ;
;
(3) ∵△BDF的边长BD是△ABC边长BC的2倍,两三角形的两边互为另一三角形两边的延长线,![]() ,∵△ABC的面积为a,
,∵△ABC的面积为a,![]() .同理可得,
.同理可得,![]() ,
,![]() ,
,![]() .
. ![]() ,
,![]() ,
,![]() ,
,
∴扩展一次后得到的△DEF的面积是原来△ABC面积的7倍.
-
科目: 来源: 题型:
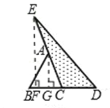
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连接DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y.

(1)求y关于x的函数关系式;
(2)若m=8,求x为何值时,y的值最大,最大值是多少?
(3)若y= ,要使△DEF为等腰三角形,m的值应为多少?
,要使△DEF为等腰三角形,m的值应为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】育才中学现有学生2870人,学校为了进一步丰富学生课余生活,拟调整兴趣活动小组,为此进行一次抽样调查.根据采集到的数据绘制的统计图(不完整)如下:请你根据图中提供的信息,完成下列问题:
(1)图1中“电脑”部分所对应的圆心角为 度;

(2)样本容量为 ;
(3)在图2中,将“体育”部分的图形补充完整;
(4)估计育才中学现有的学生中,约有 人爱好“书画”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了支援灾区学校灾后重建,我校决定再次向灾区捐助床架60个,课桌凳100套.现计划租甲、乙两种货车共8辆,将这些物质运往灾区,已知一辆甲货车可装床架5个和课桌凳20套, 一辆乙货车可装床
架10个和课桌凳10套.
(1)学校安排甲、乙两种货车可一次性把这些物资运到灾区有哪几种方案?
(2)若甲种货车每辆要付运输费1200元,乙种货车要付运输费1000元,则学校应选择哪种方案,使运输费
最少?最少运费是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我省教育厅下发了《在全省中小学幼儿园广泛深入开展节约教育》的通知,通知中要求各学校全面持续开展“光盘行动”.某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度(程度分为:“A—了解很多”,“B—了解较多”,“C—了解较少”,“D—不了解”),对本市一所中学的学生进行了抽样调查,我们将这次调查的结果绘制成以下两幅统计图.

根据以上信息,解答下列问题:
(1)本次抽样调查了多少名学生?
(2)补全两幅统计图;
(3)若该中学共有1 800名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较多”的有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个实际问题的函数图象的形状与y=
 的形状相同,且顶点坐标是(4,-2),那么它的函数解析式为( ).
的形状相同,且顶点坐标是(4,-2),那么它的函数解析式为( ).
A.y=
B.y= 或y=
或y= 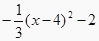
C.y=
D.y= 或y=
或y= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程: ①
 ; ②
; ② ; ③x2-y2=4;④5(x+y)=7(x+y);⑤2x2=3;⑥
; ③x2-y2=4;④5(x+y)=7(x+y);⑤2x2=3;⑥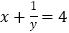 .其中是二元一次方程的是______(填序号).
.其中是二元一次方程的是______(填序号).
相关试题

