【题目】如图1,边形![]() 为菱形,点
为菱形,点![]() 为对角线
为对角线![]() 上的一个动点,连接
上的一个动点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,若![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.


参考答案:
【答案】(1)见解析;(2)60°
【解析】
(1)根据菱形的性质得出∠BCE=∠DCE,BC=CD,AB∥CD,推出∠AFD=∠CDE,证△BCE≌△DCE,推出∠CBE=∠CDE即可.(2)由(1)可知,∠EDC=∠EBC,通过DE=EC从而得出∠ DCA=30°,从而得出答案
证明:
(1)∵四边形ABCD是菱形,
∴∠BCE=∠DCE,BC=CD,AB∥CD,
∴∠AFD=∠CDE,
∵BC=CD,∠BCE=∠DCE,CE=CE
∴△BCE≌△DCE,
∴∠CBE=∠CDE,
∵∠AFD=∠CDE,
∴∠AFD=∠CBE.
(2)∵DE=CE;
∴∠ EDC=∠ ECD
由(1)知∠EDC=∠ EBC,∠ CAD=∠ CAB,
设∠EDC=∠ ECD=∠ CBE=x;
∵AB∥CD,
∴∠DCB=∠CBF=2x,
∵BE⊥AF,
∴∠EBF=∠EBC+∠CBF=x+2x=3x=90°,则x=30°;
∴∠DAB=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(1,a),将线段OA平移至线段BC,B(b,0),a是m+6n的算术平方根,
 =3,n=
=3,n=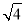 ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.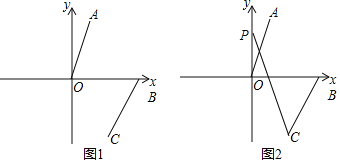
(1)直接写出A、B两点坐标为:A ,B ;
(2)如图1,连接AB、OC,求四边形AOCB的面积;
(3)如图2,若∠AOB=a,点P为y轴正半轴上一动点,试探究∠CPO与∠BCP之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将
 沿过点
沿过点 的直线
的直线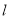 折叠,使点
折叠,使点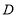 落到
落到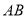 边上的
边上的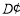 处,折痕交
处,折痕交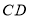 边于点
边于点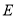 ,连接
,连接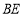 .
.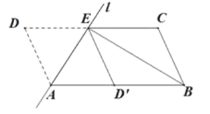
(1)求证:四边形
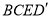 是平行四边形;
是平行四边形;(2)若
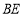 平分
平分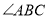 ,求证:
,求证: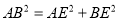 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,对称轴为直线x=1的抛物线y=
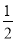 x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.(1)求点 B 的坐标和抛物线的表达式;
(2)当 AE:EP=1:4 时,求点 E 的坐标;
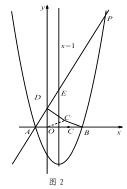
(3)如图 2,在(2)的条件下,将线段 OC 绕点 O 逆时针旋转得到 OC ′,旋转角为 α(0°<α<90°),连接 C ′D、C′B,求 C ′B+
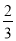 C′D 的最小值.
C′D 的最小值.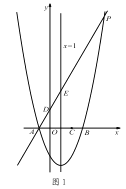
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在矩形 ABCD 中,动点 E 从点 A 出发,沿 AB→BC 方向运动,当点 E 到达点 C 时 停止运动.过点 E 作 FE⊥AE,交 CD 于 F 点,设点 E 运动路程为 x,FC=y,图②表示 y与 x 的函数关系的大致图像,则矩形 ABCD 的面积是( )
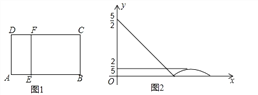
A.
 B. 5 C. 6 D.
B. 5 C. 6 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为
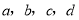 ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为 (注:
(注: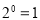 ),如图2第一行数字从左到右依次为0,1,0,1,序号为
),如图2第一行数字从左到右依次为0,1,0,1,序号为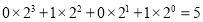 ,表示该生为5班学生,那么表示7班学生的识别图案是( )
,表示该生为5班学生,那么表示7班学生的识别图案是( )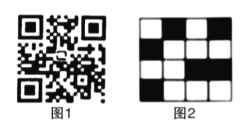
A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形 ABCD 的边长为 2,以点 A 为圆心,1 为半径作圆,点 E 是⊙A 上的任意 一点,点 E 绕点 D 按逆时针方向转转 90°,得到点 F,接 AF,则 AF 的最大值是______________
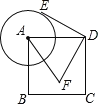
相关试题

