搜索
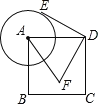
【题目】如图，已知正方形 ABCD 的边长为 2，以点 A 为圆心，1 为半径作圆，点 E 是⊙A 上的任意 一点，点 E 绕点 D 按逆时针方向转转 90°，得到点 F，接 AF，则 AF 的最大值是______________
参考答案：
【答案】
．
【解析】解：如图，过点A作∠EAB=45°交⊙A于点E，此时旋转后AF最大，过点E作EG⊥AD交DA延长线于G．在Rt△AEG中，AE=1，∠GAE=∠EAB=45°，∴EG=AG=
．∵∠ADC=∠EDF，∴∠ADE=∠CDF．在△ADE和△CDF中，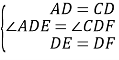
，∴△ADE≌△CDF，∴CF=AE=1，∠DCF=∠DAE=∠BAD+∠EAB=90°+45°=135°，∴点C在线段AF上，∴AF=AC+CF．∵AC是边长为2的正方形的对角线，∴AC=2
，∴AF=2+1，即：AF的最大值是2+1．故答案为：2+1．
-
科目： 来源： 题型：
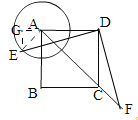
查看答案和解析>>【题目】如图1，边形
为菱形，点
为对角线
上的一个动点，连接
并延长交
于点
，连接
.(1)如图1，求证：
；(2)如图2，若
，且
，求
的度数.
-
科目： 来源： 题型：
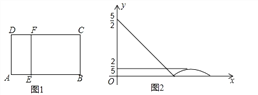
查看答案和解析>>【题目】如图①，在矩形 ABCD 中，动点 E 从点 A 出发，沿 AB→BC 方向运动，当点 E 到达点 C 时 停止运动．过点 E 作 FE⊥AE，交 CD 于 F 点，设点 E 运动路程为 x，FC＝y，图②表示 y与 x 的函数关系的大致图像，则矩形 ABCD 的面积是（ ）
A.
B. 5 C. 6 D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】利用如图1的二维码可以进行身份识别．某校建立了一个身份识别系统，图2是某个学生的识别图案，黑色小正方形表示1，白色小正方形表示0，将第一行数字从左到右依次记为
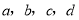，那么可以转换为该生所在班级序号，其序号为
（注：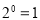
），如图2第一行数字从左到右依次为0，1，0，1，序号为
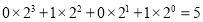，表示该生为5班学生，那么表示7班学生的识别图案是（ ）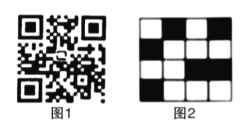
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】用一个平面去截正方体（如图），下列关于截面（截出的面）形状的结论：
①可能是锐角三角形；②可能是钝角三角形；
③可能是长方形；④可能是梯形．
其中正确结论的是______（填序号）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】【题目】如图①，一次函数 y＝
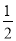x - 2 的图像交 x 轴于点 A，交 y 轴于点 B，二次函数 y＝
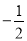x2 bx c的图像经过 A、B 两点，与 x 轴交于另一点 C．（1）求二次函数的关系式及点 C 的坐标；
（2）如图②，若点 P 是直线 AB 上方的抛物线上一点，过点 P 作 PD∥x 轴交 AB 于点 D，PE∥y 轴交 AB 于点 E，求 PD＋PE 的最大值；
（3）如图③，若点 M 在抛物线的对称轴上，且∠AMB＝∠ACB，求出所有满足条件的点 M的坐标．
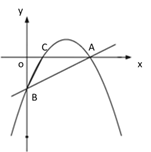
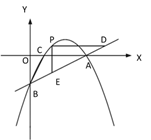
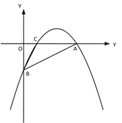
① ② ③
-
科目： 来源： 题型：
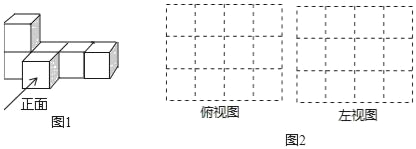
查看答案和解析>>【题目】（1）如图1是由大小相同的小立方块搭成的几何体，请在图2的方格中画出从上面和左面看到的该几何体的形状图．（只需用2B铅笔将虚线化为实线）
（2）若要用大小相同的小立方块搭一个几何体，使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同，则搭这样的一个几何体最多需要 个小立方块．
相关试题
