【题目】某中学七![]() 班共有45人,该班计划为每名学生购买一套学具,超市现有A、B两种品牌学具可供选择
班共有45人,该班计划为每名学生购买一套学具,超市现有A、B两种品牌学具可供选择![]() 已知1套A学具和1套B学具的售价为45元;2套A学具和5套B学具的售价为150元.
已知1套A学具和1套B学具的售价为45元;2套A学具和5套B学具的售价为150元.
![]() 、B两种学具每套的售价分别是多少元?
、B两种学具每套的售价分别是多少元?
![]() 现在商店规定,若一次性购买A型学具超过20套,则超出部分按原价的6折出售
现在商店规定,若一次性购买A型学具超过20套,则超出部分按原价的6折出售![]() 设购买A型学具a套
设购买A型学具a套![]() 且不超过30套,购买A、B两种型号的学具共花费w元.
且不超过30套,购买A、B两种型号的学具共花费w元.
![]() 请写出w与a的函数关系式;
请写出w与a的函数关系式;
![]() 请帮忙设计最省钱的购买方案,并求出所需费用.
请帮忙设计最省钱的购买方案,并求出所需费用.
参考答案:
【答案】(1)A、B两种学具每套的售价分别是25和20元;(2)![]() ,
,![]() ;
;![]() 购买45套B型学具所需费用最省钱,所需费用为900元.
购买45套B型学具所需费用最省钱,所需费用为900元.
【解析】
(1)设A种品牌的学具售价为x元,B种品牌的学具售价为y元,根据1套A学具和1套B学具的售价为45元,2套A学具和5套B学具的售价为150元,列出二元一次方程组解答即可;
(2)①根据总花费=购买A型学具的费用+购买B型学具的费用,列出函数关系式即可;
②分两种情况进行比较即可,第一种情况:由函数关系式可知a=30时花费已经最低,需要费用950元;第二种情况:购买45套B型学具需要900元.
解:![]() 设A种品牌的学具售价为x元,B种品牌的学具售价为y元,根据题意有,
设A种品牌的学具售价为x元,B种品牌的学具售价为y元,根据题意有,
![]() ,解之可得
,解之可得![]() ,
,
所以A、B两种学具每套的售价分别是25和20元;
![]() 因为
因为![]() ,其中购买A型学具的数量为a,
,其中购买A型学具的数量为a,
则购买费用![]()
![]() ,
,
即函数关系式为:![]() ,
,![]() ;
;
![]() 符合题意的还有以下情况:
符合题意的还有以下情况:
Ⅰ、以![]() 的方案购买,因为-5<0,所以
的方案购买,因为-5<0,所以![]() 时,w为最小值,
时,w为最小值,
即![]() 元
元![]() ;
;
Ⅱ、由于受到购买A型学具数量的限制,购买A型学具30套w已是最小,
所以全部购买B型学具45套,此时![]() 元
元![]() 元,
元,
综上所述,购买45套B型学具所需费用最省钱,所需费用为:900元.
故答案为:(1)A、B两种学具每套的售价分别是25和20元;(2)①w=-5a+1100,(20<a≤30);②购买45套B型学具所需费用最省钱,所需费用为900元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)

(2)

(3)

(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣2x﹣3.
(1)该二次函数图象的对称轴为;
(2)判断该函数与x轴交点的个数,并说明理由;
(3)下列说法正确的是(填写所有正确说法的序号)
①顶点坐标为(1,﹣4);
②当y>0时,﹣1<x<3;
③在同一平面直角坐标系内,该函数图象与函数y=﹣x2+2x+3的图象关于x轴对称. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且
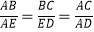 .
.
(1)求证:∠BAE=∠CAD;
(2)求证:△ABE∽△ACD. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:小明根据学习函数的经验,对函数
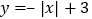 的图象与性质进行了探究.
的图象与性质进行了探究.下面是小明的探究过程,请你解决相关问题:
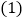 在函数
在函数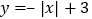 中,自变量x可以是任意实数;
中,自变量x可以是任意实数;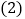 如表y与x的几组对应值:
如表y与x的几组对应值:X

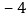
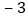
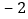
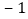
0
1
2
3
4

Y

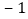
0
1
2
3
2
1
a
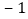

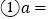 ______;
______; 若
若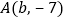 ,
,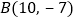 为该函数图象上不同的两点,则
为该函数图象上不同的两点,则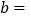 ______;
______;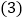 如图,在平面直角坐标系中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象:
如图,在平面直角坐标系中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象: 该函数有______
该函数有______ 填“最大值”或“最小值”
填“最大值”或“最小值” ;并写出这个值为______;
;并写出这个值为______; 求出函数图象与坐标轴在第二象限内所围成的图形的面积;
求出函数图象与坐标轴在第二象限内所围成的图形的面积; 观察函数
观察函数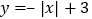 的图象,写出该图象的两条性质.
的图象,写出该图象的两条性质.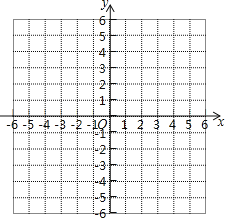
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.根据以上信息解决下列问题:
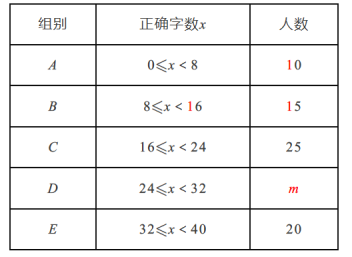

(1)在统计表中,m= ,n= ,并补全直方图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 度;
(3)若该校共有964名学生,如果听写正确的个数少于24个定为不合格,请你估算这所学校本次比赛听写不合格的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
相关试题

