搜索
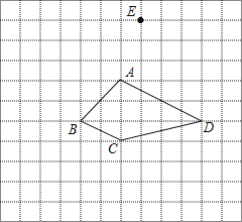
【题目】如图，方格纸中每个小方格都是边长为1的正方形，四边形ABCD的顶点与点E都是格点．
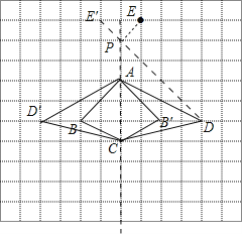
（1）作出四边形ABCD关于直线AC对称的四边形AB′CD′；
（2）求四边形ABCD的面积；
（3）若在直线AC上有一点P，使得P到D、E的距离之和最小，请作出点P（请保留作图痕迹），且求出PC=______．
参考答案：
【答案】（1）见解析；（2）9；（3）见解析，5
【解析】
（1）根据要求画出图形即可；
（2）对角线垂直的四边形的面积=对角线乘积的一半求解；
（3）作点E关于直线AC的对称点E′，连接DE′交直线AC于P，点P即为所求，再得出PC.
解：（1）四边形AB′CD′如图所示；
（2）S四边形ABCD=
×6×3=9；
（3）如图，点P即为所求，此时PC=5．
故答案为5．
-
科目： 来源： 题型：
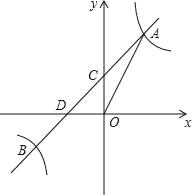
查看答案和解析>>【题目】如图，反比例函数y=
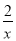的图象与一次函数y=kx+b的图象交于点A，B，点A、B的横坐标分别为1，﹣2，一次函数图象与y轴的交于点C，与x轴交于点D．（1）求一次函数的解析式；
（2）对于反比例函数y=
，当y＜﹣1时，写出x的取值范围；（3）在第三象限的反比例图象上是否存在一个点P，使得S△ODP=2S△OCA？若存在，请求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形连接AC交EF于G，下列结论: ①BE＝DF，②∠DAF＝15°，③AC⊥EF，④BE+DF＝EF，⑤EC＝FG；其中正确结论有( )个
A.2B.3C.4D.5
-
科目： 来源： 题型：
查看答案和解析>>【题目】将长为20cm，宽为8cm的长方形白纸，按如图所示的方式粘合起来，粘合部分的宽为3cm.
(1)根据题意，将下面的表格补充完整.
白纸张数x(张)
1
2
3
4
5
…
纸条总长度y(cm)
20
54
71
…
（2）直接写出y与x的关系式.
(3）要使粘合后的长方形总面积为1656cm2，则需用多少张这样的白纸?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是圆O的直径，O为圆心，AD、BD是半圆的弦，且∠PDA=∠PBD．延长PD交圆的切线BE于点E
（1）证明：直线PD是⊙O的切线.
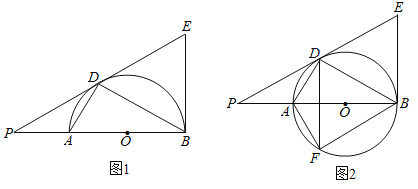
（2）如果∠BED=60°，
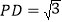，求PA的长．（3）将线段PD以直线AD为对称轴作对称线段DF，点F正好在圆O上，如图2，求证：四边形DFBE为菱形．
-
科目： 来源： 题型：
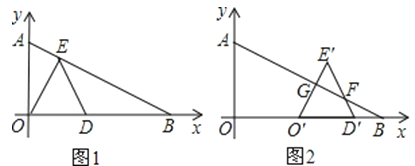
查看答案和解析>>【题目】在Rt△ABO中，∠AOB=90°，OA=
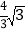，OB=4，分别以OA、OB边所在的直线建立平面直角坐标系，D为x轴正半轴上一点，以OD为一边在第一象限内作等边△ODE．（1）如图①，当E点恰好落在线段AB上时，求E点坐标；
（2）在（Ⅰ）问的条件下，将△ODE沿x轴的正半轴向右平移得到△O′D′E′，O′E′、D′E′分别交AB于点G、F（如图②）求证OO′=E′F；
（3）若点D沿x轴正半轴向右移动，设点D到原点的距离为x，△ODE与△AOB重叠部分的面积为y，请直接写出y与x的函数关系式．
-
科目： 来源： 题型：
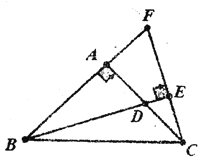
查看答案和解析>>【题目】如图，等腰直角三角形ABC中，∠BAC＝90°，D是AC的中点，EC⊥BD于E，交BA的延长线于F，若BF＝12，则△BDC的面积是______
相关试题
