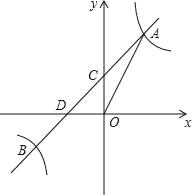
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于点A,B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
的图象与一次函数y=kx+b的图象交于点A,B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
(1)求一次函数的解析式;
(2)对于反比例函数y=![]() ,当y<﹣1时,写出x的取值范围;
,当y<﹣1时,写出x的取值范围;
(3)在第三象限的反比例图象上是否存在一个点P,使得S△ODP=2S△OCA?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=x+1;(2)当﹣2<x<0时,y<﹣1;(3)点P的坐标为:(﹣1,﹣2).
【解析】试题分析:(1)由点A.B的横坐标分别为1,2,求得A(1,2),B(2,1),由于点A.B在一次函数y=kx+b的图象上,列方程组即可得到结论;
(2)根据图象即可得到结论;
(3)存在,根据一次函数的解析式得到D(1,0),C(0,1),设P(m,n),根据![]() 列方程即可得到结论.
列方程即可得到结论.
试题解析:(1)∵点A.B的横坐标分别为1,2,
∴y=2,或y=1,
∴A(1,2),B(2,1),
∵点A.B在一次函数y=kx+b的图象上,
∴![]()
∴![]()
∴一次函数的解析式为:y=x+1;
(2)由图象得知:y<1时,写出x的取值范围是2<x<0;
(3)存在,
对于y=x+1,当y=0时,x=1,当x=0时,y=1,
∴D(1,0),C(0,1),
设P(m,n),
![]()
![]()
∴n=2,
∵点P在反比例图象上,
∴m=1,
∴P(1,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动12米到B处,测得∠EBF=30°,∠CBD=45°,sin∠CAD=
 .
.(1)求旗杆EF的高;
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.

-
科目: 来源: 题型:
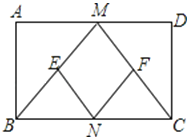
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠1=∠2,AE⊥OB于E,BD⊥OA于D,交点为C,则图中全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形连接AC交EF于G,下列结论: ①BE=DF,②∠DAF=15°,③AC⊥EF,④BE+DF=EF,⑤EC=FG;其中正确结论有( )个

A.2B.3C.4D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.

(1)根据题意,将下面的表格补充完整.
白纸张数x(张)
1
2
3
4
5
…
纸条总长度y(cm)
20
54
71
…
(2)直接写出y与x的关系式.
(3)要使粘合后的长方形总面积为1656cm2,则需用多少张这样的白纸?
-
科目: 来源: 题型:
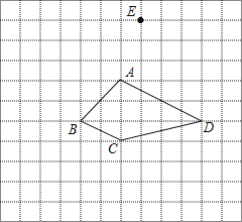
查看答案和解析>>【题目】如图,方格纸中每个小方格都是边长为1的正方形,四边形ABCD的顶点与点E都是格点.
(1)作出四边形ABCD关于直线AC对称的四边形AB′CD′;
(2)求四边形ABCD的面积;
(3)若在直线AC上有一点P,使得P到D、E的距离之和最小,请作出点P(请保留作图痕迹),且求出PC=______.
相关试题

