【题目】如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C,点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )
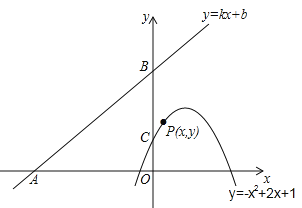
A. 1.4 B. 2.5 C. 2.8 D. 3
参考答案:
【答案】C
【解析】分析:由A、B两点的坐标,利用待定系数法可求得直线解析式;过P作PH⊥AB于点H,过H作HQ⊥x轴,过P作PQ⊥y轴,两垂线交于点Q,则可证明△PHQ∽△BAO,设H(m, ![]() m+3),利用相似三角形的性质可得到d与x的函数关系式,设C点关于抛物线对称轴的对称点为C′,由对称的性质可得CE=C′E,则可知当F、E、C′三点一线且C′F与AB垂直时CE+EF最小,由C点坐标可确定出C′点的坐标,利用所求函数关系式可求得d的值,即可求得CE+EF的最小值.
m+3),利用相似三角形的性质可得到d与x的函数关系式,设C点关于抛物线对称轴的对称点为C′,由对称的性质可得CE=C′E,则可知当F、E、C′三点一线且C′F与AB垂直时CE+EF最小,由C点坐标可确定出C′点的坐标,利用所求函数关系式可求得d的值,即可求得CE+EF的最小值.
详解: (1)由题意可得
![]() ,解得
,解得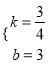 ,
,
∴直线解析式为y=![]() x+3;
x+3;
过P作PH⊥AB于点H,过H作HQ⊥x轴,过P作PQ⊥y轴,两垂线交于点Q,
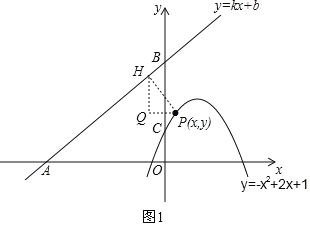
则∠AHQ=∠ABO,且∠AHP=90°,
∴∠PHQ+∠AHQ=∠BAO+∠ABO=90°,
∴∠PHQ=∠BAO,且∠AOB=∠PQH=90°,
∴△PQH∽△BOA,
∴![]() ,
,
设H(m, ![]() m+3),则PQ=xm,HQ=
m+3),则PQ=xm,HQ=![]() m+3(x+2x+1),
m+3(x+2x+1),
∵A(4,0),B(0,3),
∴OA=4,OB=3,AB=5,且PH=d,
∴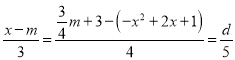
整理消去m可得d=![]() ,
,
∴d与x的函数关系式为d=![]() ,
,
设C点关于抛物线对称轴的对称点为C′,由对称的性质可得CE=C′E,
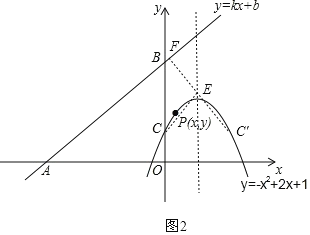
∴CE+EF=C′E+EF,
∴当F. E.C′三点一线且C′F与AB垂直时CE+EF最小,
∵C(0,1),
∴C′(2,1),
由(2)可知当x=2时,d=![]() =2.8,
=2.8,
即CE+EF的最小值为2.8.
点睛:
本题为二次函数的综合应用,涉及待定系数法、相似三角形的判定和性质、二次函数的性质、轴对称的性质等知识.注意待定系数法的应用,构造相似三角形是解题的重要步骤,确定出E点的位置是解题的关键.本题考查知点较多,综合性较强,难度适中.
-
科目: 来源: 题型:
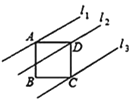
查看答案和解析>>【题目】如图,直线l1,l2,l3分别过正方形ABCD的三个顶点A,D,C,且相互平行,若l1,l2的距离为2,l2,l3的距离为4,则正方形的对角线长为_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(0,5), B(a,b),且a,b满足b=
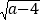 +
+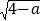 -1.
-1.(1)如图,求线段AB的长;
(2)如图,直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=-6,求OP2-OC2的值;
(3)如图,若点D(1,0),求∠DAO +∠BAO的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形
 的边长是1米;
的边长是1米;
(1)若设图中最大正方形
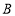 的边长是
的边长是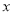 米,请用含
米,请用含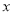 的代数式分别表示出正方形
的代数式分别表示出正方形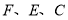 的边长
的边长(2)观察图形的特点可知,长方形相对的两边是相等的(即
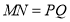 ,
, 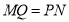 )请根据以上结论,求出
)请根据以上结论,求出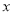 的值
的值(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙工程队单独铺设分别需要10天、15天完成,如果两队从同一位置开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,还要多少天完成?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若线段
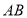 上有一点
上有一点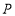 ,当
,当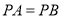 时,则称点
时,则称点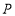 为线段
为线段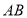 的中点.已知数轴上
的中点.已知数轴上 ,
,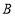 两点对应数分别为
两点对应数分别为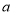 和
和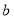 ,
,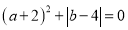 ,
,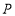 为数轴上一动点,对应数为
为数轴上一动点,对应数为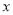 .
.(1)若点
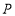 为线段
为线段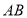 的中点,则
的中点,则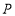 点对应的数
点对应的数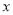 为______.若
为______.若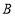 为线段
为线段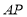 的中点时则
的中点时则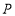 点对应的数
点对应的数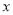 为______.
为______.(2)若点
 、点
、点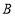 同时向左运动,它们的速度都为1个单位长度/秒,与此同时点
同时向左运动,它们的速度都为1个单位长度/秒,与此同时点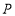 从-16处以2个单位长度/秒向右运动.
从-16处以2个单位长度/秒向右运动.①设运动的时间为
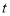 秒,直接用含
秒,直接用含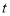 的式子填空
的式子填空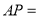 ______;
______;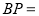 ______.
______.②经过多长时间后,点
 、点
、点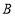 、点
、点 三点中其中一点是另外两点的中点?
三点中其中一点是另外两点的中点? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)5+(﹣6)+3﹣(﹣9)+(﹣4)﹣7
(2)(﹣2)2﹣8÷(﹣2)﹣4×|﹣5|
(3)﹣22÷
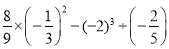
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,4),B(4,0),C(10,0),点P在直线AB上,且∠OPC=90,则点P的坐标为________________.
相关试题

