搜索
【题目】如图，两张宽度相等的纸条叠放在一起，重叠部分构成四边形ABCD．
（1）求证：四边形ABCD是菱形；
（2）若纸条宽3cm，∠ABC=60°，求四边形ABCD的面积．
参考答案：
【答案】（1）见解析；（2）四边形ABCD的面积=6
cm2．
【解析】
（1）首先可判断重叠部分为平行四边形，且两条纸条宽度相同；再由平行四边形的面积可得邻边相等，则重叠部分为菱形．
（2）解直角三角形求得菱形的边长，根据平行四边形的面积公式求得即可．
（1）过点A作AE⊥BC于E，AF⊥CD于F，
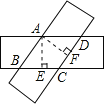
∵两条纸条宽度相同，
∴AE=AF．
∵AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形．
∵SABCD=BCAE=CDAF．
又∵AE=AF．
∴BC=CD，
∴四边形ABCD是菱形；
（2）在Rt△AEB中，∠AEB=90°，∠ABC=60°，AE=3cm，
∴AB=
=2cm，
∴BC=2cm，
∴四边形ABCD的面积=AEBC=6cm2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】以点A为顶点作两个等腰直角三角形（△ABC，△ADE），如图1所示放置，使得一直角边重合，连接BD，CE．
（1）说明BD=CE；
（2）延长BD，交CE于点F，求∠BFC的度数；
（3）若如图2放置，上面的结论还成立吗？请简单说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，∠ABC=90°，AB=3，BC=4，DC=12，AD=13，求四边形ABCD的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A、B、C的坐标分别为（-1，3）、（-4，1）、（-2，1），将△ABC沿一确定方向平移得到△A1B1C1，点B的对应点B1的坐标是（1，2），则点A1，C1的坐标分别是（ ）
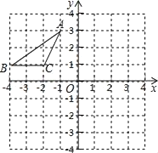
A.A1（4，4），C1（3，2）B.A1（3，3），C1（2，1）
C.A1（4，3），C1（2，3）D.A1（3，4），C1（2，2）
-
科目： 来源： 题型：
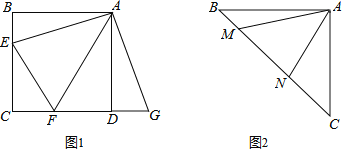
查看答案和解析>>【题目】（1）如图，正方形ABCD中，点E，F分别在边BC，CD上，∠EAF=45°，延长CD到点G，使DG=BE，连结EF，AG．求证：EF=FG．
（2）如图，等腰直角三角形ABC中，∠BAC=90°，AB=AC，点M，N在边BC上，且∠MAN=45°，若BM=1，CN=3，求MN的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD的面积为20cm2，对角线交于点O；以AB、AO为邻边做平行四边形AOC1B，对角线交于点O1；以AB、AO1为邻边做平行四边形AO1C2B；…依此类推，则平行四边形AO4C5B的面积为（ ）
A.
cm2 B. 
cm2 C. 
cm2 D. 
cm2 -
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的袋子中装有若干个除颜色外均相同的小球，小明每次从袋子中摸出一个球，记录下颜色，然后放回，重复这样的试验1000次，记录结果如下：
实验次数n
200
300
400
500
600
700
800
1000
摸到红球次数m
151
221
289
358
429
497
568
701
摸到红球频率
0.75
0.74
0.72
0.72
0.72
0.71
a
b
（1）表格中a=________，b=_________；
（2）估计从袋子中摸出一个球恰好是红球的概率约为________；（精确到0.1）
（3）如果袋子中有14个红球，那么袋子中除了红球，还有多少个其他颜色的球？
相关试题
