【题目】我们给出如下定义,如果一个四边形有一条对角线能将其分成一个等边三角形和一个直角三角形,那么这个四边形叫做等垂四边形,这条对角线叫做这个四边形的等垂对角线.
(1)已知![]() 是四边形
是四边形![]() 的等垂对角线,
的等垂对角线,![]() ,
,![]() 均为钝角,且
均为钝角,且![]() 比
比![]() 大
大![]() ,那么
,那么![]() ________.
________.
(2)如图,已知![]() 与
与![]() 关于直线
关于直线![]() 对称,
对称,![]() 、
、![]() 两点分别在
两点分别在![]() 、
、![]() 边上,
边上,![]() ,
,![]() ,
,![]() .求证:四边形
.求证:四边形![]() 是等垂四边形。
是等垂四边形。

参考答案:
【答案】(1)110°或150°;(2)见解析.
【解析】
(1)由题意分∠D=90°与∠DCA=90°两种情况,并利用四边形内角和定理求解即可;
(2)连接![]() ,先利用SAS证明
,先利用SAS证明![]() ,再证明
,再证明![]() 是等边三角形,最后利用勾股定理的逆定理证明
是等边三角形,最后利用勾股定理的逆定理证明![]() 是直角三角形即可.
是直角三角形即可.
解:(1)![]() 或
或![]() .
.
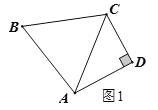
如图1,当∠D=90°时,设![]() =x°,则
=x°,则![]() =(x-10)°,根据四边形内角和定理可得:
=(x-10)°,根据四边形内角和定理可得:
x+x-10+90+60=360,解得x=110,即![]() 110°;
110°;
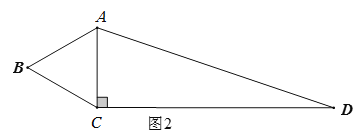
如图2,当∠DCA=90°时,![]() 60°+90°=150°;
60°+90°=150°;
故答案为![]() 或
或![]() .
.
(2)证明:如图3,连接![]() .
.
∵![]() 和
和![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是直角三角形,
是直角三角形,
∴四边形![]() 是等垂四边形.
是等垂四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 在平面直角坐标系内,顶点的坐标分别为
在平面直角坐标系内,顶点的坐标分别为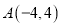 ,
,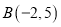 、
、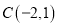 .
.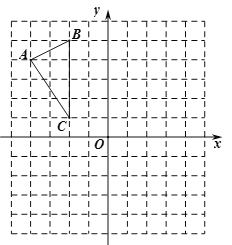
(1)平移
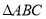 ,使点
,使点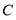 移到点
移到点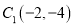 ,画出平移后的
,画出平移后的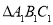 ,并写出点
,并写出点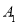 的坐标.
的坐标.(2)将
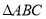 绕点
绕点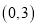 旋转
旋转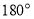 ,得到
,得到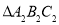 ,画出旋转后的
,画出旋转后的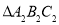 ,并写出点
,并写出点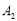 的坐标.
的坐标.(3)求(2)中的点
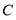 旋转到点
旋转到点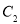 时,点
时,点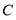 经过的路径长(结果保留
经过的路径长(结果保留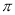 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方体的块数最多是( )

A. 9 B. 10 C. 11 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB与直线CD相交于点O,OE平分
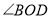 .
.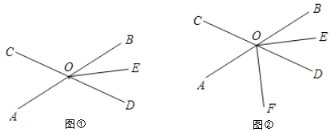
(1)如图①,若
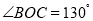 ,求
,求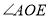 的度数;
的度数;(2)如图②,射线OF在
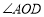 内部.
内部.①若
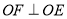 ,判断OF是否为
,判断OF是否为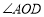 的平分线,并说明理由;
的平分线,并说明理由;②若OF平分
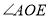 ,
,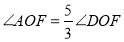 ,求
,求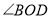 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆锥的底面半径为10 cm,高为10
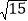 cm.
cm.(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上一点A出发绕圆锥侧面一周回到SA上的点M处,且SM=3AM,求它所走的最短距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用小立方块搭一个几何体,使它从正面、上面看到的形状图如图所示,从上面看到的形状图的小正方形中的字母表示在该位置小立方块的个数.试回答下列问题:

(1)a,b,c各表示几?
(2)这个几何体最少有几个小立方块搭成?最多呢?
(3)当d=e=1,f=2时,画出这个几何体从左面看到的形状图.
相关试题

