【题目】如图所示,在正方形![]() 中,
中,![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于
于![]() 连接
连接![]() .
.
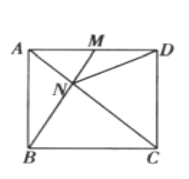
(1)证明:无论![]() 运动到
运动到![]() 上的何处,都有
上的何处,都有![]() ;
;
(2)当![]() 运动到何处时,
运动到何处时,![]() ?
?
(3)若![]() 从
从![]() 到
到![]() 再从
再从![]() 到
到![]() ,在整个运动过程中,
,在整个运动过程中,![]() 为多少时,
为多少时,![]() 是等腰三角形?
是等腰三角形?
参考答案:
【答案】(1)见解析;(2)![]() ;(3)DM=0或6或
;(3)DM=0或6或![]()
【解析】
(1)先根据正方形的性质可得![]() ,再根据三角形全等的判定定理即可得证;
,再根据三角形全等的判定定理即可得证;
(2)先根据正方形的性质得出![]() ,再根据三角形的面积公式可得
,再根据三角形的面积公式可得![]() ,从而可得
,从而可得![]() ,然后利用平行线分线段成比例定理推论可得
,然后利用平行线分线段成比例定理推论可得![]() ,由此即可得;
,由此即可得;
(3)根据等腰三角形的定义分①![]() ②
②![]() ③
③![]() 三种情况,再分别根据正方形的性质、相似三角形的判定与性质、线段的和差求解即可得.
三种情况,再分别根据正方形的性质、相似三角形的判定与性质、线段的和差求解即可得.
(1)![]() 四边形
四边形![]() 是正方形
是正方形
![]()
在![]() 和
和![]() 中,
中,
![]()
则无论![]() 运动到
运动到![]() 上的何处,都有
上的何处,都有![]() ;
;
(2)![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是正方形
是正方形
![]() ,
,![]()
![]() ,即
,即![]()
![]()
即当![]() 时,
时,![]() ;
;
(3)若![]() 是等腰三角形,分以下三种情况:
是等腰三角形,分以下三种情况:
①若![]() ,此时
,此时![]() 与
与![]() 重合,
重合,![]()
②若![]() ,此时
,此时![]() 与
与![]() 重合,
重合,![]()
③若![]() ,此时点
,此时点![]() 在
在![]() 上,如图所示:
上,如图所示:
![]() 四边形
四边形![]() 是正方形
是正方形
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
又![]()
![]()
![]()
综上,当![]() 为0或
为0或![]() 或
或![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】河南省政府为促进农业发展,加快农村建设,计划扶持兴建一批新型钢管装配式大棚,如图1所示线段AB、BD分别为大棚的墙高和跨度,AC表示保温板的长,已知墙高AB为3米,墙面与保温板所成的角∠BAC=150°,在点D处测得A点、C点的仰角分别为9°,15.6°,如图2所示求保温板AC的长是多少米?(精确到0.1米)(参考数据:sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28,
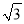 ≈1.73)
≈1.73)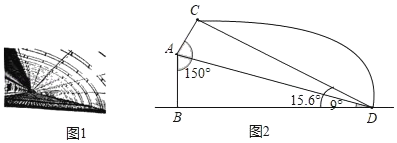
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点M、N分别是x轴y轴上的动点,点P、Q是某个函数图象上的点,当四边形MNPQ为正方形时,称这个正方形为此函数的“梦幻正方形”例如:如图1所示,正方形MNPQ是一次函数y=﹣x+2的其中一个“梦幻正方形”.
(1)若某函数是y=x+5,求它的图象的所有“梦幻正方形”的边长;
(2)若某函数是反比例函数y=
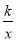 (k<0)(如图2所示),它的图象的“梦幻正方形”ABCD,D(﹣4,m)(m<4)在反比例函数图象上,求m的值及反比例函数的解析式.
(k<0)(如图2所示),它的图象的“梦幻正方形”ABCD,D(﹣4,m)(m<4)在反比例函数图象上,求m的值及反比例函数的解析式.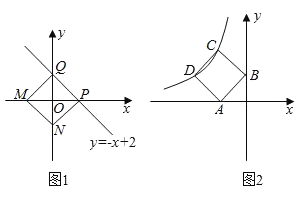
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节前夕,某批发部从厂家购进A、B两种礼盒,已知购进2个A礼盒和3个B礼盒共花520元;购进3个A礼盒和2个B礼盒共花费480元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该批发部经理购进这两种礼盒恰好用去4800元购进A种礼盒最多18个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)已知销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使A、B两种礼盒全部售出后所有方案获利均相同,m的值应是多少?此时这个批发部获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx+c与x轴交于A、B两点,A(﹣5,0),与y轴交于C(0,﹣5),并且对称轴x=﹣3.
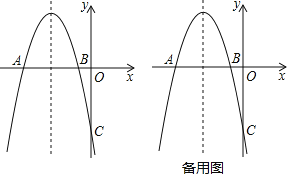
(1)求抛物线的解析式;
(2)P在x轴上方的抛物线上,过P的直线y=x+m与直线AC交于点M,与y轴交于点N,求PM+MN的最大值;
(3)点D为抛物线对称轴上一点,
①当△ACD是以AC为直角边的直角三角形时,求D点坐标;
②若△ACD是锐角三角形,求点D的纵坐标的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线M:y=-
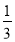 x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )
x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )A.45°B.60°C.90°D.120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,弦AB垂直平分半径OC,垂足为D.若点P是⊙O上异于点A,B的任意一点,则∠APB=( )
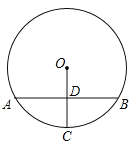
A.30°或60°B.60°或150°C.30°或150°D.60°或120°
相关试题

