【题目】在平面直角坐标系中,O是坐标原点,矩OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8),点P是y轴上的一个动点,将△OAP沿AP翻折得到:△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F.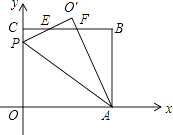
(1)当O′落在直线BC上时,求折痕AP的长.
(2)当点P在y轴正半轴上时,若△PCE与△POA相似,求直线AP的解析式;
(3)在点P的运动过程中,是否存在某一时刻,使得 ![]() ?若存在,求点P坐标;若不存在,请说明理由.
?若存在,求点P坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:图1,当O′落在直线BC上时,在RT△ABO′中,∵AO′=10,AB=8,
∴BO′= ![]() =
= ![]() =6,
=6,
∵△APO′是由△AOP翻折,
∴可以设PO=PO′=x,
在RT△PCO′中,∵PO′2=PC2+CO′2,
∴x2=(8﹣x)2+42,
∴x=5,
∴AP= ![]() =
= ![]() =5
=5 ![]()
(2)
解:当∠CPE=∠APO时,
∵∠CPE=∠APO=∠APO′=60°,
∴OP= ![]() OA=
OA= ![]() ,
,
设直线AP为y=kx+b,由题意 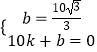 解得
解得 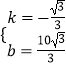 ,
,
∴直线AP为y=﹣ ![]() x+
x+ ![]() .
.
当∠CPE=∠OAP时,∠CEP=∠APO=∠APO′,此时AP∥EC,显然不可能
(3)
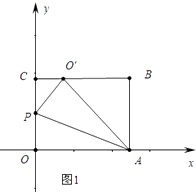
解:情形1如图2中,
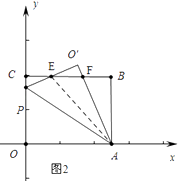
∵CE= ![]() BC=2,
BC=2,
∴BE=8,AE= ![]() =8
=8 ![]() ,EO′=
,EO′= ![]() =2
=2 ![]() ,
,
设OP=x,在RT△PCE中,∵PE2=PC2+CE2,
∴(x﹣2 ![]() )2=(8﹣x)2+22,
)2=(8﹣x)2+22,
∴x= ![]() ,此时P[0,
,此时P[0, ![]() ],
],
情形2如图3中,
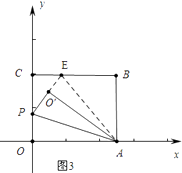
同理O′E=2 ![]() ,
,
设OP=x,在RT△PCE中,∵PE2=PC2+CE2,
∴(x+2 ![]() )2=(8﹣x)2+22,
)2=(8﹣x)2+22,
∴x= ![]() ,此时P[0,
,此时P[0, ![]() ],
],
情形3如图4中,
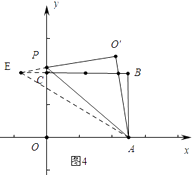
AE= ![]() =
= ![]() =4
=4 ![]() ,
,
EO′= ![]() =6
=6 ![]() ,
,
设OP=x,在RT△PCE中,∵PE2=PC2+CE2,
∴(6 ![]() ﹣x)2=(x﹣8)2+22,
﹣x)2=(x﹣8)2+22,
∴x= ![]() ,此时P[0,
,此时P[0, ![]() ],
],
情形4如图5中,
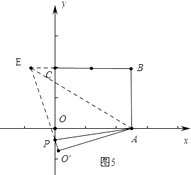
设OP=x,在RT△PCE中,∵PE2=PC2+CE2,
∴(6 ![]() ﹣x)2=(x+8)2+22,
﹣x)2=(x+8)2+22,
∴x= ![]() ,此时P[0,
,此时P[0, ![]() ].
].
【解析】(1)先在RT△ABO′求出BO′,设PO=PO′=x,在RT△PCO′中利用勾股定理解决即可.(2)当∠CPE=∠APO时得∠CPE=∠APO=∠APO′=60°求出OP= ![]() OA即可.当∠CPE=∠OAP时,∠CEP=∠APO=∠APO′,此时AP∥EC,显然不可能.(3)分四种情形讨论,在RT△PCE中利用E2=PC2+CE2列出方程求解 .
OA即可.当∠CPE=∠OAP时,∠CEP=∠APO=∠APO′,此时AP∥EC,显然不可能.(3)分四种情形讨论,在RT△PCE中利用E2=PC2+CE2列出方程求解 .
【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识,掌握对应角相等,对应边成比例的两个三角形叫做相似三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:(A组:x<155; B组:155≤x<160; C组:160≤x<165; D组165≤x<170;E组:x≥170)
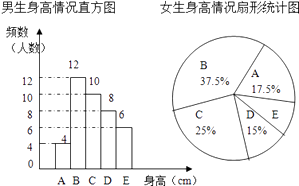
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在组,中位数在组.
(2)样本中,女生的身高在E组的人数有人.
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:小华遇到这样一个问题:
已知:如图1,在△ABC中,三边的长分别为AB= ,AC=
,AC=  ,BC=2,求∠A的正切值.
,BC=2,求∠A的正切值.
小华是这样解决问题的:
如图2所示,先在一个正方形网格(每个小正方形的边长均为1)中画出格点△ABC(△ABC三个顶点都在小正方形的顶点处),然后在这个正方形网格中再画一个和△ABC相似的格点△DEF,从而使问题得解.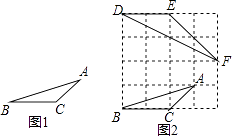
(1)如图2,△DEF中与∠A相等的角为 , ∠A的正切值为 .
(2)参考小华的方法请解决问题:若△LMN的三边分别为LM=2,MN=2 ,LN=2
,LN=2  ,求∠N的正切值.
,求∠N的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司装修需用A型板材240块,B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(如图是裁法一的裁剪示意图)
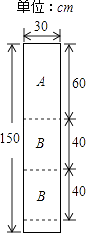
裁法一
裁法二
裁法三
A型板材块数
1
2
0
B型板材块数
2
m
n
(1)上表中,m= , n=;
(2)若裁完剩余的部分可以拼接成A型或B型板材使用,则至少需要几张标准板材?
(3)若裁完剩余的部分不能拼接成A型或B型板材使用,已知用170张标准板材,可以完成装修任务.请通过计算写出两种剪裁方案(要求:①其中一种方案三种剪裁方法都使用,另一种方案只用到两种剪裁方法;②每种方案需写出使用各种裁剪方法裁剪标准板的张数). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2017次相遇在边( )上.

A. AB B. BC C. CD D. DA
-
科目: 来源: 题型:
查看答案和解析>>【题目】(提出问题)
如图①,点
 、
、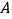 、
、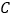 在同一条直线上,
在同一条直线上,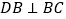 ,
,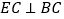 ,且
,且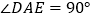 ,
,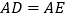 ,易证
,易证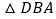 ≌
≌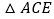 .
.(类比探究)
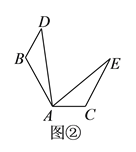
(
 )如图②,在
)如图②,在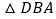 和
和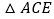 中,
中,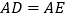 ,若
,若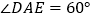 ,
,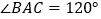 ,
,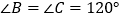 .求证:
.求证: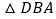 ≌
≌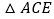 .
.(知识应用)
(
 )如图②,在
)如图②,在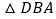 和
和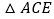 中,
中,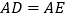 ,若
,若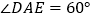 ,
,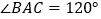 ,
,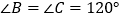 ,若
,若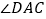 的度数是
的度数是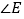 的
的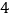 倍,则
倍,则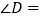 __________
__________ .
.(数学思考)
(
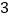 )如图②,在
)如图②,在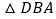 和
和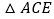 中,
中,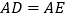 ,若
,若 ,
,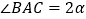 ,当
,当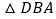 ≌
≌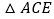 时,
时,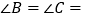 __________.(结果用含有
__________.(结果用含有 的代数式表示)
的代数式表示)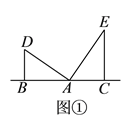
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+mx+m-2=0.
(1)求证:无论m取何值,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1,x2,当m=3时,求
 的值.
的值.
相关试题

