【题目】如图,在平行四边形ABCD中,E为CD上一点,连结AE,BD,且AE,BD交于点F,S△DEF∶S△ABF=4∶25,求DE∶EC的值.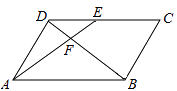
参考答案:
【答案】解:∵四边形ABCD是平行四边形,
∴AB∥CD.
∴△DEF∽△BAF.
∴ ![]() .
.
∴ ![]()
又∵AB=CD,
∴DE:EC=2:3.
【解析】根据平行四边形得出对边平行,即可证得△DEF∽△BAF.再根据相似三角形的面积比等于相似比的平方,求出DE与AB的比值,再根据AB=CD,即可得出结果。
【考点精析】通过灵活运用平行四边形的性质和相似三角形的判定与性质,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.
-
科目: 来源: 题型:
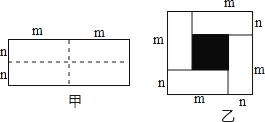
查看答案和解析>>【题目】已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均剪成四个小长方形,然后拼成如图乙所示的一个大正方形.
(1)你认为图乙中的阴影部分的正方形的边长= ;
(2)请用两种不同的方法求图乙中阴影部分的面积:
方法一:
方法二:
(3)观察图乙,请你写出下列代数式之间的等量关系:
(m+n)2、(m﹣n)2、mn
.
(4)根据(3)题中的等量关系,解决如下问题:若a+b=8,ab=7,求a﹣b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在数轴上表示的数是-8,点
在数轴上表示的数是-8,点 在数轴上表示的数是16.若点
在数轴上表示的数是16.若点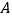 以6个单位长度/秒的速度向右匀速运动,同时点
以6个单位长度/秒的速度向右匀速运动,同时点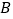 以2个单位长度/秒的速度向左匀速运动.问:当
以2个单位长度/秒的速度向左匀速运动.问:当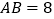 时,运动时间为多少秒?
时,运动时间为多少秒?
A. 2秒B. 13.4秒C. 2秒或4秒D. 2秒或6秒
-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级一班小张陪妈妈到水果市场购买水果,在一个水果摊前听到妈妈与售货员的对话:
妈妈:“售货员同志,请帮我买些上次梨.”
售货员:“大妈,您上次买的那种梨都卖完了,我们还没来得及进货,我建议这次您买些新进的苹果,价格比梨贵一点,不过苹果的营养价值更高.”
妈妈:“好,你们的服务态度和服务质量我很满意,这次我照上次一样,也买30元钱的苹果吧.”回家后对照前后两次的电脑小票,小张发现:每千克苹果的单价价是梨的单价的1.5倍,苹果的重量比梨轻2.5千克.
小张根据上面的对话和发票,求出了梨和苹果的单价,你知道梨和苹果的单价各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一工程招标时,接到甲.乙两工程队的投标书,每施工一天,需付甲工程队工程款1.5万元,乙工程队工程款1.1万元.目前有三种施工方案:
方案一:甲队单独完成此项工程刚好如期完成;
方案二:乙队单独完成此项工程比规定日期多5天;
方案三:若甲.乙两队合作4天,剩下的工程由乙队单独做也正好如期完成.
哪一种方案既能如期完工又最节省工程款?
-
科目: 来源: 题型:
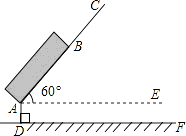
查看答案和解析>>【题目】如图是春运期间的一个回家场景。一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,点A到地面的距离AD=8cm,旅行箱与水平面AE成60°角,求拉杆把手处C到地面的距离(精确到1cm).(参考数据:
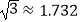 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.

解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(
即∠ =∠ ( )
∴∠3=∠
∴AD∥BE( )
相关试题

