【题目】如图,圆![]() 与
与![]() 的斜边
的斜边![]() 相切于点
相切于点![]() ,与直角边
,与直角边![]() 相交于
相交于![]() 两点,连结
两点,连结![]() ,已知
,已知![]() ,圆
,圆![]() 的半径为6,弧
的半径为6,弧![]() 的长度为
的长度为![]() 。
。
(1)求证:![]() ∥
∥![]() ;
;
(2)若![]() ,求线段
,求线段![]() 的长度。
的长度。
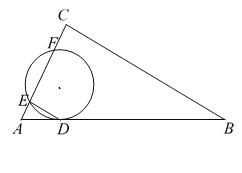
参考答案:
【答案】(1)证明见解析(2)CA=10![]() ,CB=30
,CB=30
【解析】试题分析:(1)要证明DE∥BC,可证明∠EDA=∠B,由弧DE的长度为4π,可以求得∠DOE的度数,再根据切线的性质可求得∠EDA的度数,即可证明结论.
(2)根据90°的圆周角对的弦是直径,可以求得EF,的长度,借用勾股定理求得AE与CF的长度,即可得到答案.
试题解析:(1)证明:连接OE,OF,OD
∵圆![]() 的半径为6,弧
的半径为6,弧![]() 的长度为
的长度为![]()
∴![]() 即∠EOD=n=60°,OD=OE=6
即∠EOD=n=60°,OD=OE=6
∴△EOD为等边三角形
∴∠OED=∠EDO =∠EOD =60°
∵圆![]() 与
与![]() 的斜边
的斜边![]() 相切于点
相切于点![]()
∴OD⊥AB即∠ODA =90°
∴∠EDA =∠ODA -∠ODE =30°=∠B
∴![]() ∥
∥![]()

(2)解:∵![]() ∥
∥![]() ,∠C =90°∴
,∠C =90°∴
∴∠AED =∠C=90°,∠FED =180°-∠C=90°
∴FD为圆![]() 的直径,即FD过点O
的直径,即FD过点O
∴在Rt△EDF中,∠EFD =90°-∠EDF=30°
∴FD=12,EF=6![]()
∴在Rt△AED中,EA=2![]()
∴CE=AF=8![]()
∴CA=AF+AE=10![]() ,CB=
,CB=![]() AC=30
AC=30
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD的对角线相交于点O,AC=
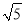 ,CD=1,
,CD=1,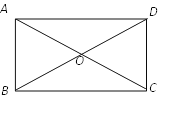
(1)尺规作图:作∠ABC的平分线交AD于点E,连结CE;
(2)判断线段BE与CE的关系,并证明你的判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有40个数据,共分成6组,第1~4组的频数分别为10,5,7,6,第5组的频率是0.1,则第6组的频数是( )
A.8
B.28
C.32
D.40 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边长分别为 6 和 1,则这个等腰三角形的周长为( )
A. 13 B. 8 C. 10 D. 8 或 13
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=
 (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=
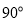 ,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.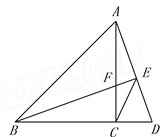
(1)求证: CF=CD;
(2)求证:
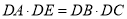 ;
; (3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】种树时,只要定出两个树坑的位置,就能使同一行树坑在同一条直线上,其中的数学道理是_____.
相关试题

