【题目】如图,在△ABC中,AC=BC,∠ACB=![]() ,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
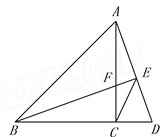
(1)求证: CF=CD;
(2)求证: ![]() ;
;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
参考答案:
【答案】(1)证明见解析(2)证明见解析(3)AE,BE,CE之间满足的等量关系![]()
【解析】试题分析:(1)由垂直的定义得到∠ACB=90°,根据全等三角形的判定定理ASA可证明△BCF≌△ACD,然后根据全等三角形的性质可证明;
(2)根据相似三角形的判定证得△BED∽△ACD,然后根据相似三角形的性质可证明;
(3)在BE上截取BG=AE,连接CG,然后根据三角形全等的判定可证明△GCE是等腰直角三角形,由此可得到结果.
试题解析:(1)证明:∵∠BCA=∠ACD = 90°
∴∠FBC+∠D=∠CAD +∠D = 90°
∴∠FBC =∠CAD
∵AC=BC
∴△BCF≌△ACD(ASA)
∴CF=CD
(2)证明:∵∠FBC =∠CAD ∠D=∠D
∴△BED∽△ACD
∴BD:AD=ED:CD
∴![]()
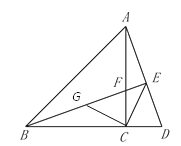
(3)AE,BE,CE之间满足的等量关系![]()
理由:在BE上截取BG=AE,连接CG,
∵∠FBC =∠CAD BC=AC
∴△BCG≌△ACE
∴GC=EC 且∠BCG=∠ACE
∴∠GCE=∠ACD= 90°
∴△GCE为等腰直角三角形
∴GC=![]() CE
CE
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边长分别为 6 和 1,则这个等腰三角形的周长为( )
A. 13 B. 8 C. 10 D. 8 或 13
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆
 与
与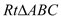 的斜边
的斜边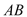 相切于点
相切于点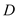 ,与直角边
,与直角边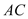 相交于
相交于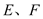 两点,连结
两点,连结 ,已知
,已知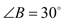 ,圆
,圆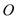 的半径为6,弧
的半径为6,弧 的长度为
的长度为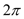 。
。(1)求证:
 ∥
∥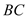 ;
;(2)若
 ,求线段
,求线段 的长度。
的长度。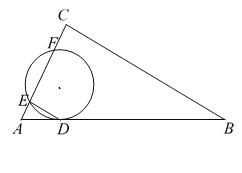
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=
 (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】种树时,只要定出两个树坑的位置,就能使同一行树坑在同一条直线上,其中的数学道理是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的内角和为 720°,则这个多边形是( )
A. 三角形 B. 四边形 C. 五边形 D. 六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某糕点厂中秋节前要制作一批盒装月饼,每盒中2块大月饼和4块小月饼,制作1块大月饼要用0.05kg面粉,制作1块小月饼要用0.02kg面粉,若现共有面粉540kg,设可以生产x盒盒装月饼,则可列方程为_____.
相关试题

