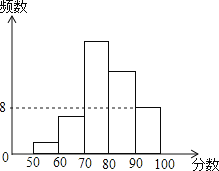
【题目】某校组织部分学参加安全知识竞赛,并将成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%,12%,40%,28%,第五组的频数是8.则:①参加本次竞赛的学生共有100人;②第五组的百分比为16%;③成绩在70-80分的人数最多;④80分以上的学生有14名;其中正确的个数有( )
A.1个B.2个C.3个D.4个
参考答案:
【答案】B
【解析】
根据频数分布直方图中每一组内的频率总和等于1,可得出第五组的百分比,又因为第五组的频数是8,即可求出总人数,根据总人数即可得出80分以上的学生数,从而得出正确答案.
①参加本次竞赛的学生共有8÷(1-4%-12%-40%-28%)=50(人),此项错误;
②第五组的百分比为1-4%-12%-40%-28%=16%,此项正确;
③成绩在70-80分的人数最多,此项正确;
④80分以上的学生有50×(28%+16%)=22(名),此项错误;
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)求售价x的范围;
(3)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-
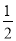 x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数y=-
 +|x|的图象与性质.
+|x|的图象与性质.
小军根据学习函数的经验,对函数y=- +|x|的图象与性质进行了探究.
+|x|的图象与性质进行了探究.
下面是小军的探究过程,请补充完整:
(1)函数y=- +|x|的自变量x的取值范围是 ;
+|x|的自变量x的取值范围是 ;
(2)表是y与x的几组对应值.x
-2
-1.9
-1.5
-1
-0.5
0
1
2
3
4
…
y
2
1.60
0.80
0
-0.72
-1.41
-0.37
0
0.76
1.55
…
在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;

(3)观察图象,函数的最小值是 ;
(4)进一步探究,结合函数的图象,写出该函数的一条性质(函数最小值除外): . -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:
 .
.(2)解不等式
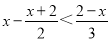 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
(3)解方程组:
 .
. -
科目: 来源: 题型:
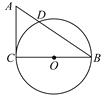
查看答案和解析>>【题目】如图,在Rt△ACB中,∠C=90°,AC=3 cm,BC=4 cm,以BC为直径作⊙O交AB于点D.
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问当点E在什么位置时,直线ED与⊙O相切?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一过点C的动圆⊙O与斜边AB相切于动点P,连接CP.
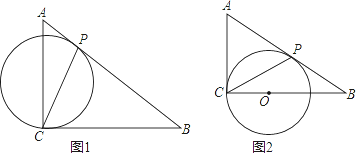
(1)当⊙O与直角边AC相切时,如图2所示,求此时⊙O的半径r的长;
(2)随着切点P的位置不同,弦CP的长也会发生变化,试求出弦CP的长的取值范围.
(3)当切点P在何处时,⊙O的半径r有最大值?试求出这个最大值.
相关试题

