【题目】如图1,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一过点C的动圆⊙O与斜边AB相切于动点P,连接CP.
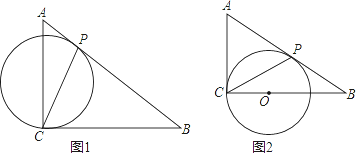
(1)当⊙O与直角边AC相切时,如图2所示,求此时⊙O的半径r的长;
(2)随着切点P的位置不同,弦CP的长也会发生变化,试求出弦CP的长的取值范围.
(3)当切点P在何处时,⊙O的半径r有最大值?试求出这个最大值.
参考答案:
【答案】(1) r=![]() ;(2)
;(2) ![]() ≤PC≤4;(3)
≤PC≤4;(3) ![]() .
.
【解析】
试题分析:(1)先根据勾股定理求出AB的长,再由切线的性质求出PB的长,过P作PQ⊥BC于Q,过O作OR⊥PC于R,根据PQ∥AC得出PC的长,再由△COR∽△CPQ即可得出r的值;
(2)根据最短PC为AB边上的高,最大PC=BC=4即可得出结论;
(3)当P与B重合时,圆最大.这时,O在BD的垂直平分线上,过O作OD⊥BC于D,由BD=![]() BC=2,由于AB是切线可知∠ABO=90°,∠ABD+∠OBD=∠BOD+∠OBD=90°,故可得出∠ABC=∠BOD,根据锐角三角函数的定义即可得出结论.
BC=2,由于AB是切线可知∠ABO=90°,∠ABD+∠OBD=∠BOD+∠OBD=90°,故可得出∠ABC=∠BOD,根据锐角三角函数的定义即可得出结论.
试题解析:(1)如图1,

∵在Rt△ACB中,∠ACB=90°,AC=3,BC=4,
∴AB=![]() .
.
∵AC、AP都是圆的,圆心在BC上,AP=AC=3,
∴PB=2,
过P作PQ⊥BC于Q,过O作OR⊥PC于R,
∵PQ∥AC,
∴![]() ,
,
∴PQ=![]() ,BQ=
,BQ=![]() ,
,
∴CQ=BC-BQ=![]() ,
,
∴PC=![]() ,
,
∵点O是CE的中点,
∴CR=![]() PC=
PC=![]() ,
,
∴∠PCE=∠PCE,∠CRO=∠CQP,
∴△COR∽△CPQ,
∴![]() ,即
,即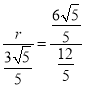 ,解得r=
,解得r=![]() ;
;
(2)∵最短PC为AB边上的高,即PC=![]() =
=![]() ,最大PC=BC=4,
,最大PC=BC=4,
∴![]() ≤PC≤4;
≤PC≤4;

(3)如图2,当P与B重合时,圆最大.O在BD的垂直平分线上,过O作OD⊥BC于D,由BD=![]() BC=2,
BC=2,
∵AB是切线,
∴∠ABO=90°,
∴∠ABD+∠OBD=∠BOD+∠OBD=90°,
∴∠ABC=∠BOD,
∴![]() =sin∠BOD=sin∠ABC=
=sin∠BOD=sin∠ABC=![]() ,
,
∴OB=![]() ,即半径最大值为
,即半径最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P为直线l外一点,点A、B、C为直线上三点,PA=2cm,PB=3cm,PC=4cm,则点P到直线l的距离为( )
A.等于2cm B.小于2cm C.大于2cm D.不大于2cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】若收入100元记作+100元,那么﹣100元表示________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是( )
A. 3 B. 6 C. 9 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好地了解某区近阶段九年级学生的中考目标,某研究机构设计了如下调查问卷(单选):你的中考目标是哪一个?
A.升入四星普通高中;B.升入三星级普通高中;C.升入五年制高职类学校; D.升入中等职业类学校;E.等待初中毕业,不想再读书了.
在随机调查了某区3000名九年级学生中的部分学生后,统计整理并制作了如下的统计图.根据有关信息解答下列问题:

(1)此次共调查了 名学生,计算扇形统计图中
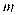 = .
= .(2) 补全条形统计图。
(3) 请你估计其中有多少名学生选择升入四星普通高中。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若α,β是方程x2﹣2x﹣2=0的两个实数根,则α2+β2的值为( )
A.10
B.9
C.8
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个菱形的四个内角度数之比依次为1:2:3:4,这个事件是( )
A. 必然事件 B. 随机事件 C. 不可能事件 D. 以上都不是
相关试题

